
【题目】在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x,y′)的纵坐标满足y′=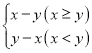 ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
(1)请直接写出点(3,5)的“关联点”的坐标 ;
(2)如果点P在函数y=x﹣2的图象上,其“关联点”Q与点P重合,求点P的坐标;
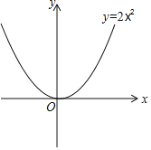
(3)如果点M(m,n)的“关联点”N在函数y=2x2的图象上,当0≤m≤2时,求线段MN的最大值.
【答案】(1)(3,2);(2)(4,2);(3)当m≥n时,线段MN的最大值是14;当m<n时,线段MN的最大值是2.
【解析】
(1)根据关联点的定义,可得答案;
(2)根据关联点的定义,可得Q点的坐标,根据点在函数图象上,可得方程,根据解方程,可得答案;
(3)根据关联点的定义,可得N的坐标,根据平行于y轴的直线上两点间的距离,可得二次函数,根据二次函数的性质,可得答案.
解:(1)∵3<5,根据关联点的定义,y′=5﹣3=2,
∴点(3,5)的“关联点”的坐标(3,2),
故答案为:(3,2);
(2)∵点P在函数y=x﹣2的图象上,
∴点P的坐标为(x,x﹣2).
∵x>x﹣2,根据关联点的定义,点Q的坐标为(x,2).
又∵点P与点Q重合,
∴x﹣2=2,解得x=4,
∴点P的坐标是(4,2);
(3)点M(m,n)的“关联点”N,由关联点的定义,得
第一种情况:当m≥n时,点N的坐标为(m,m﹣n),
∵N在函数y=2x2的图象上,
∴m﹣n=2m2,n=﹣2m2+m,即yM=﹣2m2+m,yN=2m2,
∴MN=|yM﹣yN|=|﹣4m2+m|,
①当0≤m≤![]() ,﹣4m2+m≥0,
,﹣4m2+m≥0,
MN=﹣4m2+m=﹣4(m﹣![]() )2+
)2+![]() ,
,
∴当m=![]() 时,线段MN的最大值是
时,线段MN的最大值是![]() ;
;
②当![]() <m≤2时,﹣4m2+m<0,
<m≤2时,﹣4m2+m<0,
MN=4m2﹣m=4(m﹣![]() )2﹣
)2﹣![]() ,当m=2时,线段MN的最大值是14;
,当m=2时,线段MN的最大值是14;
第二种情况:当m<n时,点N的坐标为(m,n﹣m),
∵N在函数y=2x2的图象上,
∴n﹣m=2m2,即n=2m2+m,
∴yM=2m2+m,yN=2m2,
∴MN=|yM﹣yN|=|m|,
∵0≤m≤2,
∴MN=m,
∴当m=2时,线段MN的最大值是2;
综上所述:当m≥n时,线段MN的最大值是14;当m<n时,线段MN的最大值是2.


科目:初中数学 来源: 题型:
【题目】某种型号汽车油箱容量为40L,每行驶100km耗油10L.设一辆加满油的该型号汽车行驶路程为x(km),行驶过程中油箱内剩余油量为y(L)
(1)求y与x之间的函数表达式;
(2)为了有效延长汽车使用寿命,厂家建议每次加油时油箱内剩余油量不低于油箱容量的四分之一,按此建议,求该辆汽车最多行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由:
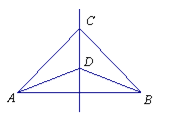
解:∵ CD是线段AB的垂直平分线
∴ AC=BC,AD=DB( )
在△ADC和△BDC中,
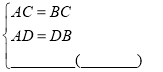
∴△ADC≌和△BDC( ).
∴ ∠CAD=∠CBD( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安爱知中学为了全面提高学生的综合素养,学校组织了音乐,篮球,跆拳道,美术共四个社团,初学生积极参加(每个学生限报一项),参加社团的学生共有![]() 人,其中音乐社团有
人,其中音乐社团有![]() 人参加,篮球社团参加的人数比音乐社团参加的人数的两倍少
人参加,篮球社团参加的人数比音乐社团参加的人数的两倍少![]() 人,跆拳道社团参加的人数比篮球社团参加的人数一半多1人
人,跆拳道社团参加的人数比篮球社团参加的人数一半多1人
(1)篮球社团有 人.(用含![]() 的式子表示)
的式子表示)
(2)求篮球社团比跆拳道社团多多少人?(用含![]() 的式子表示)
的式子表示)
(3)若![]() ,求美术社团的人数
,求美术社团的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程![]()
(1)求证:方程总有两个不相等的实数根。
(2)m为何整数时,此方程的两个根都是正整数?
(3)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
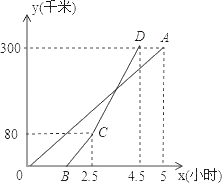
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com