
����Ŀ�����Ƕ��壺��һ��Խ���ȶ���һ��ԽDz���ȵ��ı��ν������ȶԽ��ı�������
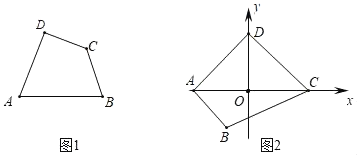
��1����֪����ͼ1���ı���ABCD�����ȶԽ��ı���������A����C����A��75������D��85�������C���� ����
��2����֪�������ȶԽ��ı�����ABCD�У���DAB��60������ABC��90����AB��4��AD��3����Խ���AC�ij���
��3����֪����ͼ2����ƽ��ֱ������ϵxOy�У��ı���ABCD�����ȶԽ��ı�����������A����2��0����C��2��0����B����1����![]() ������D��y���ϣ�������y��ax2+bx+c��a��0������A��D���ҵ���2��x��2ʱ������y��ax2+bx+cȡ���ֵΪ3���������ϵ��a��ֵ��
������D��y���ϣ�������y��ax2+bx+c��a��0������A��D���ҵ���2��x��2ʱ������y��ax2+bx+cȡ���ֵΪ3���������ϵ��a��ֵ��
���𰸡���1��115������2��AC�ij�Ϊ![]() ��
��![]() ����3��a����
����3��a����![]() ��1��
��1��![]()
��������
��1����B=��D=85�������C=360��-2��85��-75��=115����������⣻
��2������ͼ1��![]() AE=8��DE=5�������
AE=8��DE=5�������![]() ����AC�����������ͼ2��ͬ���ɵ�
����AC�����������ͼ2��ͬ���ɵ�![]() BC=BF+CF
BC=BF+CF![]() �����ɹ��ɶ��������AC�ij���
�����ɹ��ɶ��������AC�ij���
��3���������ɵó���ADC=��ABC=90�������D��0��2��������A��D��������꣬����������ߵĽ���ʽΪy=ax2+��2a+1��x+2��������������ǣ���x=2ʱ������y=ax2+��2a+1��x+2ȡ�����ֵΪ3�������![]() ����-2��x��2ʱ���ڶ��㴦ȡ�����ֵ�������
����-2��x��2ʱ���ڶ��㴦ȡ�����ֵ�������![]()
�⣺��1����B����D��85�������C��360����2��85����75����115����
�ʴ�Ϊ115����
��2������ͼ1����B����D��90��ʱ���ӳ�AD��BC���ڵ�E��
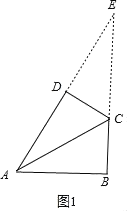
�ߡ�DAB��60����
���E��30����
�֡�AB��4��AD��3
��BE��4![]() ��AE��8��DE��5��
��AE��8��DE��5��
��![]() ��
��
��BC��BE��CE��4![]() ��
��![]() ��
��
��![]() ��
�� ��
��![]() ��
��
����ͼ����A����C��60��ʱ����D�ֱ���DE��AB��E��DF��BC�ڵ�F��
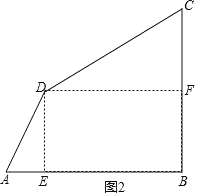
�ߡ�DAB����BCD��60����
�֡�AB��4��AD��3��
��![]() ��DE��BF��
��DE��BF��![]() ��
��
��![]() ��
��
��![]() ��
��
��BC��CF+BF��![]() ��
��
��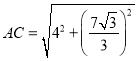 ��
��![]() ��
��
�ۺ����Ͽɵ�AC�ij�Ϊ![]() ��
��![]() ��
��
��3����A����2��0����C��2��0����B����1����![]() ����
����
��AB��2��BC��2![]() ��AC��4��
��AC��4��
��AB2+BC2��AC2��
���ABC��90����
��AD��CD��AB��BC��
���BAD����BCD��
���ı���ABCD�����ȶԽ��ı�����
���ADC����ABC��90����
��D��0��2��
��������y��ax2+bx+c����A����2��0����D��0��2����
��![]() ��
��
��ã�c��2��b��2a+1��
�������ߵĽ���ʽΪy��ax2+��2a+1��x+2��
��x��2ʱ������y��ax2+��2a+1��x+2ȡ�����ֵΪ3��
��4a+4a+2+2��3��
��a����![]() ��
��
��ʱ�����ߵĶԳ���Ϊx��3��
��![]() �������⣬
�������⣬
�����κ���y��ax2+��2a+1��x+2�ڶ���ȡ�����ֵ3�����У�
![]() ��
��
��ã�a����1+![]() ��a����1��
��a����1��![]() ��
��
��a����1+![]() ʱ���Գ�����ֱ��x��2���Ҳ࣬�������⣬��ȥ��
ʱ���Գ�����ֱ��x��2���Ҳ࣬�������⣬��ȥ��
��![]() ��
��
�ۺ����Ͽɵ�a����![]() ��1��
��1��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���о����κ���y=-(x-m)2-m+1(mΪ����)����ʱ���½��ۣ����������ͼ��Ķ���ʼ����ֱ��y=-x+1�ϣ��ڴ���һ��m��ֵ��ʹ�ú���ͼ��Ķ�����![]() ����������㹹�ɵ���ֱ�������Σ��۵�A(x1,y1)���B(x2,y2)�ں���ͼ���ϣ���x1<x2��x1+x2>2m����y1<y2���ܵ�-1<x<2ʱ��y��x�������������m��ȡֵ��ΧΪm��2���д�����۵�����ǣ� ��
����������㹹�ɵ���ֱ�������Σ��۵�A(x1,y1)���B(x2,y2)�ں���ͼ���ϣ���x1<x2��x1+x2>2m����y1<y2���ܵ�-1<x<2ʱ��y��x�������������m��ȡֵ��ΧΪm��2���д�����۵�����ǣ� ��
A. ��B. ��C. ��D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+b��ͼ����ֱ��y��x+2�ཻ�ڵ�A��1��m������B��n��0����
��1������κ����Ľ���ʽ����д���Ò����ߵĶԳ���Ͷ������ꣻ
��2��ѡȡ�ʵ������������±�������ͼ�е�ֱ������ϵ����㻭���������ߵ�ͼ��
x | ���� | �� �� | �� �� | �� �� | �� �� | �� �� | ���� |
y | ���� | �� �� | �� �� | �� �� | �� �� | �� �� | ���� |
��3������������������ͼ�����ͼ��ֱ��д��ax2+b��x+2ʱx��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������OABC�����Ϊ9����OΪ����ԭ�㣬��A��x���ϣ���C��y���ϣ���B�ں���y��![]() (k��0��x��0)��ͼ���ϣ���P(m��n)�Ǻ���y��
(k��0��x��0)��ͼ���ϣ���P(m��n)�Ǻ���y��![]() (k��0��x��0)��ͼ������һ�㣬����P�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪE��F���������OEPF��������OABC���غϲ��ֵ����ΪS.
(k��0��x��0)��ͼ������һ�㣬����P�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪE��F���������OEPF��������OABC���غϲ��ֵ����ΪS.

(1)���B�������k��ֵ��
(2)��S��![]() ʱ�����P�����ꣻ
ʱ�����P�����ꣻ
(3)д��S����m�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���y��x2��2x+k�IJ���ͼ����ͼ��ʾ�������x��һԪ���η���x2��2x+k��0�Ľ�һ��Ϊx1��3����x2��2x+k��0��һ����x2��_____��
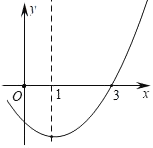
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�D��E�ֱ���AB��AC���ϵĵ㣬��F��BC���ӳ����ϣ�DE��BC������A��48������1��54������������ȷ���ǣ�������
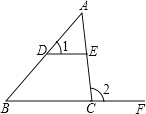
A. ��2��48��B. ��2��54��C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ������������Ĺ㷺Ӧ�ã������˿����ҵ�ĸ��ٷ�չ��������ij�ҿ�ݹ�˾��2017��3�·���5�·����Ͷ�ݵĿ���ܼ����ֱ�Ϊ10�����12.1������ּٶ��ù�˾ÿ��Ͷ�ݵĿ���ܼ�������������ͬ��
(1)��ÿ�ݹ�˾Ͷ�ݿ���ܼ�������ƽ����������
(2) ���ƽ��ÿ��ÿ������Ͷ�ݿ��0.6�������ô�ù�˾���е�21�����Ͷ��ҵ��Ա�ܷ����2017��6�·ݵĿ��Ͷ������������ܣ�����������Ҫ���Ӽ���ҵ��Ա��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������ABCD�Ķ���A������Ϊ(l,1)����B��x���������ϣ���D�ڵ�������˫����y=![]() �ϣ�����C��CE//x�ύ˫�����ڵ�E������BE�����BCE�����Ϊ________��
�ϣ�����C��CE//x�ύ˫�����ڵ�E������BE�����BCE�����Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ھ���ABCD�У����ӶԽ���AC������ABC�Ƶ�B˳ʱ����ת90��õ���EFG����������ֱ��AB����ƽ�ƣ�ֱ��EG��BC���ڵ�H������AH��CG��
��1����ͼ������AB=BC����Fƽ�Ƶ��߶�BA��ʱ���߶�AH��CG��������������ϵ��λ�ù�ϵ��ֱ��д����IJ��룻
��2����ͼ������AB=BC����Fƽ�Ƶ��߶�BA���ӳ�����ʱ����1���еĽ����Ƿ��������˵�����ɣ�
��3����ͼ������AB=nBC��n��1��ʱ���Ծ���ABCD��������֪ͬ���ı任�������߶�AH��CG��������������ϵ��λ�ù�ϵ��ֱ��д����IJ��룮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com