
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(l,1),点B在x轴正半轴上,点D在第三象限的双曲线y=![]() 上,过点C作CE//x轴交双曲线于点E,连接BE,则△BCE的面积为________.
上,过点C作CE//x轴交双曲线于点E,连接BE,则△BCE的面积为________.

【答案】7
【解析】
作辅助线,构建全等三角形:过D作GH⊥x轴,过A作AG⊥GH,过B作BM⊥HC于M,证明△AGD△DHC△CMB,根据点D的坐标表示:AG=DH=x1,由DG=BM,列方程可得x的值,表示D和E的坐标,根据三角形面积公式可得结论.
过D作GH⊥x轴,过A作AG⊥GH,过B作BM⊥HC于M,
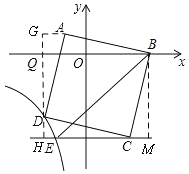
设D(x,![]() ),
),
∵四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠DCB=90°,
易得△AGD△DHC△CMB,
∴AG=DH=x1,
∴DG=BM,
∴1![]() =1x
=1x![]() ,
,
x=2,
∴D(2,3),CH=DG=BM=1![]() =4,
=4,
∵AG=DH=1x=1,
∴点E的纵坐标为4,
当y=4时,x=![]() ,
,
∴E(-![]() ,4),
,4),
∴EH=2![]() =
=![]() ,
,
∴CE=CHHE=4![]() =
=![]() ,
,
∴S△CEB=![]() CEBM=
CEBM=![]() ×
×![]() ×4=7
×4=7


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
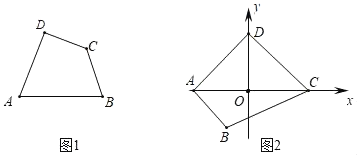
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=75°,∠D=85°,则∠C= .
(2)已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=4,AD=3.求对角线AC的长.
(3)已知:如图2,在平面直角坐标系xOy中,四边形ABCD是“等对角四边形”,其中A(﹣2,0)、C(2,0)、B(﹣1,﹣![]() ),点D在y轴上,抛物线y=ax2+bx+c(a<0)过点A、D,且当﹣2≤x≤2时,函数y=ax2+bx+c取最大值为3,求二次项系数a的值.
),点D在y轴上,抛物线y=ax2+bx+c(a<0)过点A、D,且当﹣2≤x≤2时,函数y=ax2+bx+c取最大值为3,求二次项系数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).

(1)在图中作出△ABC的外接圆(保留必要的作图痕迹,不写作法),圆心坐标为 ______;
(2)若在x轴的正半轴上有一点D,且∠ADB=∠ACB,则点D的坐标为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() 与x轴交于A、B两点,△ABC为等边三角形,∠COD=60°,且OD=OC.
与x轴交于A、B两点,△ABC为等边三角形,∠COD=60°,且OD=OC.
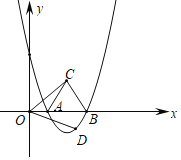
(1)A点坐标为 ,B点坐标为 ;
(2)求证:点D在抛物线上;
(3)点M在抛物线的对称轴上,点N在抛物线上,若以M、N、O、D为顶点的四边形为平行四边形,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套,设销售单价为x(x60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单价为多少元时,且销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,AF⊥BC,垂足为D.
(1)求证:∠BAE=∠CAD.
(2)若⊙O的半径为4,AC=5,CD=2,求CF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x,y′)的纵坐标满足y′=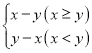 ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
(1)请直接写出点(3,5)的“关联点”的坐标 ;
(2)如果点P在函数y=x﹣2的图象上,其“关联点”Q与点P重合,求点P的坐标;
(3)如果点M(m,n)的“关联点”N在函数y=2x2的图象上,当0≤m≤2时,求线段MN的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com