【题目】如图，正方形OABC绕着点O逆时针旋转40°得到正方形ODEF，连接AF，求∠OFA的度数
科目：初中数学 来源： 题型：
【题目】如图，抛物线m：y=ax2+b（a＜0，b＞0）与x轴于点A、B（点A在点B的左侧），与y轴交于点C．将抛物线m绕点B旋转180°，得到新的抛物线n，它的顶点为C1，与x轴的另一个交点为A1．若四边形AC1A1C为矩形，则a，b应满足的关系式为（ ）
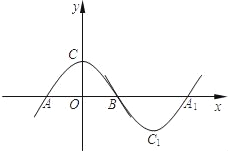
A. ab=﹣2 B. ab=﹣3 C. ab=﹣4 D. ab=﹣5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论：①这个函数图象的顶点始终在直线y=-x+1上；②存在一个m的值，使得函数图象的顶点与
轴的两个交点构成等腰直角三角形；③点A(x1,y1)与点B(x2,y2)在函数图象上，若x1<x2，x1+x2>2m，则y1<y2；④当-1<x<2时，y随x的增大而增大，则m的取值范围为m≥2其中错误结论的序号是（ ）
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为落实“美丽泰州”的工作部署，市政府计划对城区道路进行改造，现安排甲、乙两个工程队完成该改造工作.已知甲队的工作效率是乙队工作效率的
倍，甲队改造720米的道路比乙队改造同样长的道路少用4天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米？
(2)若甲队工作一天需付费用7万元，乙队工作一天需付费用5万元，若需改造的道路全长2400米，改造总费用不超过195万元，则至少安排甲队工作多少天？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小林准备进行如下操作实验：把一根长为
的铁丝剪成两段，并把每一段各围成一个正方形.
（1）若设其中的一个正方形边长为
，则另一个正方形边长为_____
；
（2）要使这两个正方形的面积之和等于
，两段长分别是多少？
（3）若要使得这两个正方形的面积之和最小，两段长分别是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+bx过点B（1，﹣3），对称轴是直线x=2，且抛物线与x轴的正半轴交于点A．
（1）求抛物线的解析式，并根据图象直接写出当y≤0时，自变量x的取值范图；
（2）在第二象限内的抛物线上有一点P，当PA⊥BA时，求△PAB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y＝ax2+b的图象与直线y＝x+2相交于点A（1，m），点B（n，0）．
（1）求二次函数的解析式，并写出该拋物线的对称轴和顶点坐标；
（2）选取适当的数据填入下表，并在图中的直角坐标系内描点画出该抛物线的图象；
x | …… |
|
|
|
|
| …… |
y | …… |
|
|
|
|
| …… |
（3）画出这两个函数的图象，并结合图象直接写出ax2+b＞x+2时x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知正方形OABC的面积为9，点O为坐标原点，点A在x轴上，点C在y轴上，点B在函数y＝
(k＞0，x＞0)的图象上，点P(m，n)是函数y＝ (k＞0，x＞0)的图象上任一点，过点P分别作x轴、y轴的垂线，垂足分别为E，F，并设矩形OEPF和正方形OABC不重合部分的面积为S.
(1)求点B的坐标和k的值；
(2)当S＝
时，求点P的坐标；
(3)写出S关于m的函数表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，正方形ABCD的顶点A的坐标为(l,1)，点B在x轴正半轴上，点D在第三象限的双曲线y=
上，过点C作CE//x轴交双曲线于点E，连接BE，则△BCE的面积为________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
