【题目】如图，在△ABC中，D、E分别是AB、AC边上的点，点F在BC的延长线上，DE∥BC，若∠A＝48°，∠1＝54°，则下列正确的是（ ）
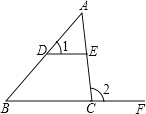
A. ∠2＝48°B. ∠2＝54°C. 
D. 
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案科目：初中数学 来源： 题型：
【题目】某品牌手机去年每台的售价y（元）与月份x之间满足函数关系：y＝﹣50x+2600，去年的月销量p（万台）与月份x之间成一次函数关系，其中1﹣6月份的销售情况如下表：
月份（x） | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
销售量（p） | 3.9万台 | 4.0万台 | 4.1万台 | 4.2万台 | 4.3万台 | 4.4万台 |
（1）求p关于x的函数关系式；
（2）求该品牌手机在去年哪个月的销售金额最大？最大是多少万元？
（3）今年1月份该品牌手机的售价比去年12月份下降了m%，而销售量也比去年12月份下降了1.5m%．今年2月份，经销商决定对该手机以1月份价格的“八折”销售，这样2月份的销售量比今年1月份增加了1.5万台．若今年2月份这种品牌手机的销售额为6400万元，求m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
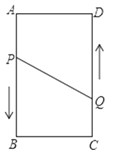
【题目】如图，A、B、C、D为矩形的四个顶点，AB=16cm，AD=6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，一直到达B为止，点Q以2 cm/s的速度向D移动．
（1）P、Q两点从出发开始到几秒？四边形PBCQ的面积为33cm2；
（2）P、Q两点从出发开始到几秒时？点P和点Q的距离是10cm．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．
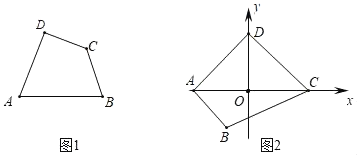
（1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A＝75°，∠D＝85°，则∠C＝ ．
（2）已知：在“等对角四边形”ABCD中，∠DAB＝60°，∠ABC＝90°，AB＝4，AD＝3．求对角线AC的长．
（3）已知：如图2，在平面直角坐标系xOy中，四边形ABCD是“等对角四边形”，其中A（﹣2，0）、C（2，0）、B（﹣1，﹣
），点D在y轴上，抛物线y＝ax2+bx+c（a＜0）过点A、D，且当﹣2≤x≤2时，函数y＝ax2+bx+c取最大值为3，求二次项系数a的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
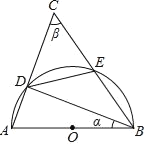
【题目】如图，以△ABC的一边AB为直径的半圆与边AC，BC分别交于点D，E，且弧DE＝弧BE，设∠ABD＝α，∠C＝β．
（1）用含β的代数式表示α，并直接写出β的取值范围；
（2）若AB＝10，BC＝12，求点O到弦BE的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，点A的坐标为（0，7），点B的坐标为（0，3），点C的坐标为（3，0）．
（1）在图中作出△ABC的外接圆（保留必要的作图痕迹，不写作法），圆心坐标为 ______；
（2）若在x轴的正半轴上有一点D，且∠ADB=∠ACB，则点D的坐标为 ______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套,设销售单价为x(x60)元，销售量为y套.
(1)求出y与x的函数关系式；
(2)当销售单价为多少元时，且销售额为14000元?
(3)当销售单价为多少元时，才能在一个月内获得最大利润，最大利润是多少?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知二次函数
的顶点P的横坐标为
，且与y轴交于点C（0，－4）．
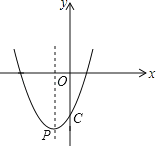
（1）求b，c的值；
（2）直线y=m(m>0)与该抛物线的交点为M，N（点M在点N的左侧）点M关于y轴的对称点为点M，点H的坐标为（3，0）．若四边形ONMH的面积为18．求点H到OM的距离；
（3）是否在对称轴的同侧存在实数m、n(m<n)，当
时，y的取值范围为
？若存在，求出m，n的值；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
