
����Ŀ����ͼ���ı���ABCD��BEFG��Ϊ�����Σ�
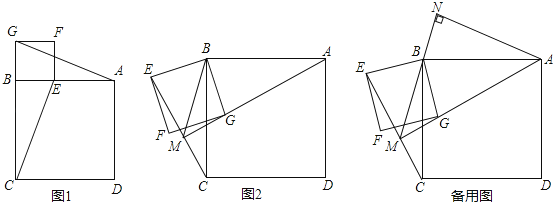
��1����ͼ1������AG��CE�����ж�AG��CE��������ϵ��λ�ù�ϵΪ�� ����ֱ��д�����
��2����������BEFG�Ƶ�B˳ʱ����ת���ǣ�0�㣼����180�㣩����ͼ2������AG��CE�ཻ�ڵ�M������MB�������������仯ʱ��AG��CE��������ϵ��λ�ù�ϵ�Ƿ����仯����˵�����ɣ�
��3���ڣ�2���������£��籸��ͼ������MB������A��AN��MB��MB���ӳ����ڵ�N����MB��3![]() ��������ABCD�ı߳�Ϊ3
��������ABCD�ı߳�Ϊ3![]() ����BN�ij���
����BN�ij���
���𰸡���1��AG��EC��AG��EC����2�����۲��䣬����������3��BN��![]() .
.
��������
��1��AG=EC��AG��EC������Ϊ����������BEFG��������ABCD�����������ε����ʵõ����Ա���ȣ�һ��ֱ����ȣ�����SAS�ó�������ABG��������CBEȫ�ȣ�����ȫ�������εĶ�Ӧ����ȣ���Ӧ����ȵõ�CE=AG����BCE=��BAG��������ͬ�ǵ������ȼ��ɵ�֤��
��2�����۲��䣬����Ϊ������SAS�ó�������ABG��������BECȫ�ȼ��ɽ�����⣻
��3����B��BP��EC��BH��AM������֤��BMƽ�֡�BME����֤��CM=![]() BN�����MC���ɽ�����⣻
BN�����MC���ɽ�����⣻
�⣺��1��AG=EC��AG��EC��
����Ϊ����ͼ1�У�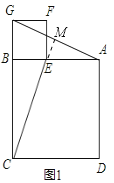
��������BEFG��������ABCD��
��GB=BE����ABG=90����AB=BC����ABC=90����
����ABG����BEC��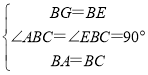 ��
��
���ABG�ա�BEC��SAS����
��CE=AG����BCE=��BAG��
�ӳ�CE��AG�ڵ�M��
���BEC=��AEM��
���ABC=��AME=90����
��AG=EC��AG��EC��
�ʴ�ΪAG=EC��AG��EC��
��2�����۲��䣮
����Ϊ����ͼ2�У���AM��BC��O��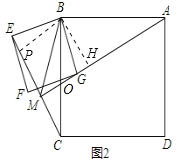
�ߡ�EBG=��ABC=90����
���ABG=��EBC��
����ABG����CEB��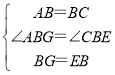 ,
,
��
���ABG�ա�CEB��SAS����
��AG=EC����BAG=��BCE��
�ߡ�BAG+��AOB=90������AOB=��COM��
���BCE+��COM=90����
���OMC=90����
��AG��EC��
��3����ͼ2�У���B��BP��EC��BH��AM��
��S��ABG=S��EBC��AG=EC��
��
![]() ECBP=
ECBP=![]() AGBH��
AGBH��
��BP=BH��
��MBΪ��EMG��ƽ���ߣ�
�ߡ�AMC=��ABC=90����
���EMB=![]() ��EMG=
��EMG=![]() ��90��=45����
��90��=45����
��ͼ3�У���NA�Ͻ�ȡNQ=NB������BQ����BH��AM��H������AC��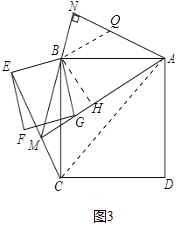
���BNQΪ����ֱ�������Σ���BQ=![]() BN��
BN��
�ߡ�AMN=45������N=90����
���AMNΪ����ֱ�������Σ���AN=MN��
��MN-BN=AN-NQ����AQ=BM��
�ߡ�MBC+��ABN=90������BAN+��ABN=90����
���MBC=��BAN��
����ABQ����BCM��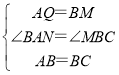 ��
��
���ABQ�ա�BCM��SAS����
��CM=BQ��
��CM=![]() BN��
BN��
�ߡ�BMH=45����BH��AM��BM=3![]()
��BH=HM=3��
��AH=![]() =6��
=6��
��AM=9��AC=3![]() ��
��
��CM=![]() =3��
=3��
��BN=![]() CM=
CM=![]() .
.


 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ4��������ֽƬABCD�۵���ʹ�õ�A���ڱ�CD���е�E�����ۺ�ΪFG����F��G�ֱ��ڱ�AD��BC�ϣ����ۺ�FG�ij���Ϊ_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪������![]() (kΪ��������
(k��������
��1���������߾�����(1,k2)����k��ֵ��
��2���������߾�����(2k,y1)�͵�(2,y2)����y1>y2����k��ȡֵ��Χ��
��3����������������ƽ��1����λ���ȵõ��������ߣ���1��x��2ʱ���������߶�Ӧ�ĺ�������Сֵ![]() ����k��ֵ��
����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ1���ڡ�ABC�У���ACB��90�㣬BC��AC����D��AB�ϣ�DE��AB��BC��E����F��AE���е�
��1��д���߶�FD���߶�FC�Ĺ�ϵ��֤����
��2����ͼ2������BDE�Ƶ�B��ʱ����ת����0�㣼����90�㣩�������������䣬�߶�FD���߶�FC�Ĺ�ϵ�Ƿ�仯��д����Ľ��۲�֤����
��3������BDE�Ƶ�B��ʱ����תһ�ܣ����BC��4��BE��2![]() ��ֱ��д���߶�BF�ķ�Χ��
��ֱ��д���߶�BF�ķ�Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1������ABCD�У�EF��GH��EF�ֱ�AB��CD�ڵ�E��F��GH�ֱ�AD��BC�ڵ�G��H����֤��![]() ��
��![]() ��
��
��2����ͼ2�������㣨1���������£���AM��BN����M��N�ֱ��ڱ�BC��CD�ϣ���![]() ����
����![]() ��ֵΪ�� ����
��ֵΪ�� ����
��3����ͼ3���ı���ABCD�У���ABC��90�㣬AB��AD��12��BC��CD��4��AM��DN����M��N�ֱ��ڱ�BC��AB�ϣ���![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����M��N�ֱ���������ABCD�ı�BC��CD�ϵĵ㣬��BM��CN�� AM��BN���ڵ�P����̽��AM��BN�Ĺ�ϵ.
��1��������ϵ_____________________����֤����
��2��λ�ù�ϵ_____________________����֤��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijƷ���ֻ�ȥ��ÿ̨���ۼ�y��Ԫ�����·�x֮�����㺯����ϵ��y����50x+2600��ȥ���������p����̨�����·�x֮���һ�κ�����ϵ������1��6�·ݵ�����������±���
�·ݣ�x�� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� |
��������p�� | 3.9��̨ | 4.0��̨ | 4.1��̨ | 4.2��̨ | 4.3��̨ | 4.4��̨ |
��1����p����x�ĺ�����ϵʽ��
��2�����Ʒ���ֻ���ȥ���ĸ��µ����۽���������Ƕ�����Ԫ��
��3������1�·ݸ�Ʒ���ֻ����ۼ۱�ȥ��12�·��½���m%����������Ҳ��ȥ��12�·��½���1.5m%������2�·ݣ������̾����Ը��ֻ���1�·ݼ۸�ġ����ۡ����ۣ�����2�·ݵ��������Ƚ���1�·�������1.5��̨��������2�·�����Ʒ���ֻ������۶�Ϊ6400��Ԫ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��̣�x��3����x��2��=|m|��
��1����֤����������ʵ��m������������������ȵ�ʵ������
��2�������̵�һ������1����m��ֵ�����̵���һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
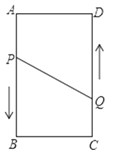
����Ŀ����ͼ��A��B��C��DΪ���ε��ĸ�������AB=16cm��AD=6cm������P��Q�ֱ�ӵ�A��Cͬʱ��������P��3cm/s���ٶ����B�ƶ���һֱ����BΪֹ����Q��2 cm/s���ٶ���D�ƶ���
��1��P��Q����ӳ�����ʼ�����룿�ı���PBCQ�����Ϊ33cm2��
��2��P��Q����ӳ�����ʼ������ʱ����P�͵�Q�ľ�����10cm��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com