
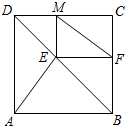
 如图,E是正方形ABCD的对角线BD上一点,EF⊥BC,EM⊥CD,垂足分别是F,M.
如图,E是正方形ABCD的对角线BD上一点,EF⊥BC,EM⊥CD,垂足分别是F,M.分析 (1)根据题意我们不难得出四边形MEFC是个矩形,因此它的对角线相等.如果连接EC,那么EC=FM,要证明AE=FM,只要证明EC=AE即可.证明AE=EC就要通过全等三角形来实现.三角形ABE和BEC中,有∠ABD=∠CBD,有AB=BC,有一组公共边BE,因此构成了全等三角形判定中的SAS,因此两三角形全等,得AE=EC,即AE=MF.
(2)根据全等三角形的性质得出∠DAE=∠DCE再解答即可.
解答 (1)证明:连接EC.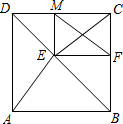
∵四边形ABCD是正方形,EF⊥BC,EM⊥CD,
∴∠MCF=∠CFE=∠CME=90°,
∴四边形EFCM为矩形.
∴FM=CE.
又BD为正方形ABCD的对角线,
∴∠ABE=∠CBE.
在△ABE和△CBE中,
$\left\{\begin{array}{l}{BE=BE}\\{∠ABE=∠CBE}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△CBE(SAS).
∴AE=EC.
∴AE=FM;
(2)由(1)得∠DAE=∠DCE,
∵$tan∠DAE=\frac{1}{3},MF=2\sqrt{10}$
设EM=k,MC=3k,
∴${k^2}+{(3k)^2}={(2\sqrt{10})^2}∴k=2$,
∴EM=2,MC=6.
可得DM=EM=2.
∴DC=8,
∴S正方形=64.
点评 本题考查了全等三角形的判定,正方形和矩形的性质等知识点,通过构建全等三角形来证明简单的线段相等是解此类题的常用方法.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:填空题
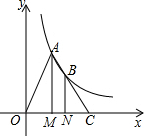 如图,点A,B在反比例函数y=$\frac{2}{x}(x>0)$的图象上,过点A,B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,则S△ACM=2.
如图,点A,B在反比例函数y=$\frac{2}{x}(x>0)$的图象上,过点A,B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,则S△ACM=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-a2)3=a6 | B. | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | C. | a6÷a3=a3 | D. | (a+4)(a-4)=a2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 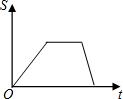 | C. | 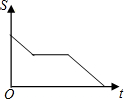 | D. | 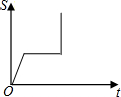 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下四个结论:①△ACD≌△BCE;②AD=BE;③∠AOB=60°;④△CPQ是等边三角形.
如图所示,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下四个结论:①△ACD≌△BCE;②AD=BE;③∠AOB=60°;④△CPQ是等边三角形.| A. | ①②③④ | B. | ②③④ | C. | ①③④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b2-4ak>0 | B. | b2-4ak=0 | C. | b2-4ak<0 | D. | b2-4ak≥0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com