
【题目】某校举办“创建全国文明城市”知识竞赛,计划购买甲、乙两种奖品共30件.其中甲种奖品每件30元,乙种奖品每件20元.
(1)如果购买甲、乙两种奖品共花费800元,那么这两种奖品分别购买了多少件?
(2)若购买乙种奖品的件数不超过甲种奖品件数的3倍,如何购买甲、乙两种奖品,使得总花费最少?
【答案】(1)甲购买了20件,乙购买了10件;(2)购买甲奖品8件,乙奖品22件,总花费最少
【解析】
(1)设甲购买了x件乙购买了y件,利用购买甲、乙两种奖品共花费了800元列方程组,然后解方程组计算即可;
(2)设甲种奖品购买了a件,乙种奖品购买了(30-a)件,利用购买乙种奖品的件数不超过甲种奖品件数的3倍,然后列不等式后确定x的范围即可得到该校的购买方案.
解:(1)设甲购买了x件,乙购买了y件,
![]() ,
,
解得![]() ,
,
答:甲购买了20件,乙购买了10件;
(2)设购买甲奖品为a件.则乙奖品为(30-a)件,根据题意可得:
30-a≤3a,
解得a≥![]() ,
,
又∵甲种奖品每件30元,乙种奖品每件20元,
总花费=30a+20(30-a)=10a+600,总花费随a的增大而增大
∴当a=8时,总花费最少,
答:购买甲奖品8件,乙奖品22件,总费用最少.


科目:初中数学 来源: 题型:
【题目】[问题解答]
两个城镇![]() 与一条公路
与一条公路![]() 位置如图①所示.现电信部门需在公路
位置如图①所示.现电信部门需在公路![]() 上修建一座信号发射塔
上修建一座信号发射塔![]() 要求发射塔
要求发射塔![]() 到两个城镇
到两个城镇![]() 与
与![]() 的距离之和最短.
的距离之和最短.
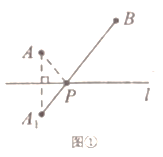
解:点![]() 作关于直线
作关于直线![]() 的对称点
的对称点![]() 连结
连结![]() ,
,
与直线![]() 的交点即为所求的点
的交点即为所求的点![]() .
.
![]() 点
点![]() 关于直线
关于直线![]() 对称,
对称,
![]() 直线
直线![]() 垂直平分
垂直平分![]()
![]()
![]()
![]() 点
点![]() 即为所求的点。(两点之间线段最短)
即为所求的点。(两点之间线段最短)
请根据以上问题解答,完成下列问题.
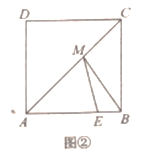
[方法运用]如图②,在正方形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上,点
上,点![]() 在对角线AC上,
在对角线AC上,
(1)当点![]() 是边
是边![]() 的中点时,则
的中点时,则![]() 的最小值为 ;
的最小值为 ;
(2)若![]() 求
求![]() 周长的最小值.
周长的最小值.
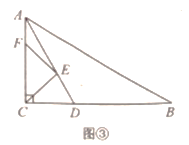
[拓展提升]如图③,在![]() 中,
中,![]() ,AD平分
,AD平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 分别在
分别在![]() 上,则
上,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 在
在![]() 上.则下列命题为真命题的是( )
上.则下列命题为真命题的是( )
A.若半径![]() 平分弦
平分弦![]() .则四边形
.则四边形![]() 是平行四边形
是平行四边形
B.若四边形![]() 是平行四边形.则
是平行四边形.则![]()
C.若![]() .则弦
.则弦![]() 平分半径
平分半径![]()
D.若弦![]() 平分半径
平分半径![]() .则半径
.则半径![]() 平分弦
平分弦![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
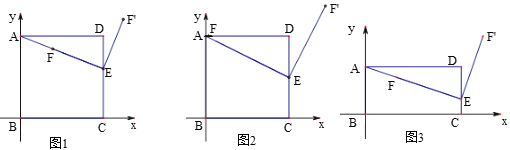
【题目】正方形ABCD的边长为4,以B为原点建立如图1平面直角坐标系中,E是边CD上的一个动点,F是线段AE上一点,将线段EF绕点E顺时针旋转90°得到EF'.
(1)如图2,当E是CD中点,![]() 时,求点F'的坐标.
时,求点F'的坐标.
(2)如图1,若![]() ,且F',D,B在同一直线上时,求DE的长.
,且F',D,B在同一直线上时,求DE的长.
(3)如图3,将正边形ABCD改为矩形,AD=4,AB=2,其他条件不变,若![]() ,且F',D,B在同一直线上时,则DE的长是_______.(请用含n的代数式表示)
,且F',D,B在同一直线上时,则DE的长是_______.(请用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
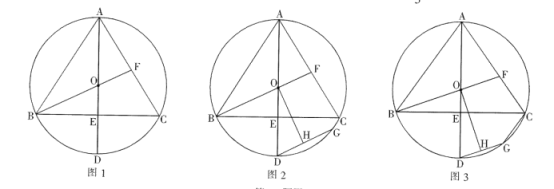
【题目】已知![]() 是
是![]() 的外接圆,AD为
的外接圆,AD为![]() 的直径,
的直径,![]() ,垂足为E,连接BO,延长BO交AC于点F.
,垂足为E,连接BO,延长BO交AC于点F.
(1)如图1,求证:![]() ;
;
(2)如图2,过点D作![]() ,交
,交![]() 于点G,点H为GD的中点,连接OH,求证:
于点G,点H为GD的中点,连接OH,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接CG,若![]() 的面积为
的面积为![]() ,求线段CG的长.
,求线段CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的门票价格如表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园,这两个部门人数分别为a和b(a≥b).若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则共需支付门票费为990元,那么这两个部门的人数a=_____;b=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数y=![]() (x>0)的图象与直线y=mx交于点A(2,2).
(x>0)的图象与直线y=mx交于点A(2,2).
(1)求k,m的值;
(2)点P的横坐标为n(n>0),且在直线y=mx上,过点P作平行于x轴的直线,交y轴于点M,交函数y=![]() (x>0)的图象于点N.
(x>0)的图象于点N.
①n=1时,用等式表示线段PM与PN的数量关系,并说明理由;
②若PN≥3PM,结合函数的图象,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年是脱贫攻坚年,为实现全员脱贫目标,某村贫困户在当地政府支持帮助下,办起了养鸡场,经过一段时间精心饲养,总量为3000只的一批鸡可以出售.现从中随机抽取50只,得到它们质量的统计数据如下:
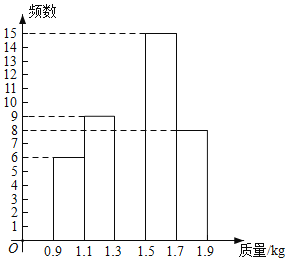
质量 | 组中值 | 数量(只) |
| 1.0 | 6 |
| 1.2 | 9 |
| 1.4 | a |
| 1.6 | 15 |
| 1.8 | 8 |
根据以上信息,解答下列问题:
(1)表中![]() ______,补全频数分布直方图;
______,补全频数分布直方图;
(2)这批鸡中质量不小于![]() 的大约有多少只?
的大约有多少只?
(3)这些贫因户的总收入达到54000元,就能实现全员脱贫目标.按15元![]() 的价格售出这批鸡后,该村贫困户能否脱贫?
的价格售出这批鸡后,该村贫困户能否脱贫?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陕西省某甜瓜基地因“规模大、品质好、品牌亮”吸引了周边大批水果批发商订购,该基地对需要送货上门且购买量在![]() (含1000kg和3000kg)的客户制定了两种销售方案(客户只能选择其中一种方案),已知该基地甜瓜批发价随市场变化波动,设某天批发价为每千克m元.
(含1000kg和3000kg)的客户制定了两种销售方案(客户只能选择其中一种方案),已知该基地甜瓜批发价随市场变化波动,设某天批发价为每千克m元.
方案一:每千克![]() 元,免运费;
元,免运费;
方案二:每千克m元,客户需支付运费1200元.
(1)请分别写出这一天按方案一、方案二购买这种甜瓜的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)当购买量x在什么范围时,选择方案二比方案一付款少;
(3)已知5月某天批发价为每千克8元,某水果批发商计划用25000元在这一天购买尽可能多的这种甜瓜并需要送货上门,那么他在这两种方案中,应选择哪一种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com