
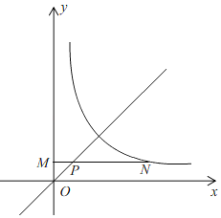
【题目】在平面直角坐标系xOy中,函数y=![]() (x>0)的图象与直线y=mx交于点A(2,2).
(x>0)的图象与直线y=mx交于点A(2,2).
(1)求k,m的值;
(2)点P的横坐标为n(n>0),且在直线y=mx上,过点P作平行于x轴的直线,交y轴于点M,交函数y=![]() (x>0)的图象于点N.
(x>0)的图象于点N.
①n=1时,用等式表示线段PM与PN的数量关系,并说明理由;
②若PN≥3PM,结合函数的图象,直接写出n的取值范围.
【答案】(1)4;1 (2)①见解析 ②![]()
【解析】
(1)将点A坐标代入双曲线解析式中和直线解析式中,求解即可得出结论;
(2)① 先求出点M,N点坐标,即可得出结论;
② 先求出点P坐标,进而表示出点M,N的坐标,得出PM,PN,利用PN≥3PM建立不等式求解即可得出结论.
(1)∵ y=![]() (x>0)的图象与直线y=mx交于点A(2,2),
(x>0)的图象与直线y=mx交于点A(2,2),
∴ k=2×2=4,2=2m,
∴ m=1,
即 k=4,m=1;
(2)①由(1)知,k=4,m=1,
∴ 双曲线的解析式为y=![]() ,直线OA的解析式为y=x,
,直线OA的解析式为y=x,
∵ n=1,
∴ P(1,1),
∵ PM//x轴,
∴ M(0,1),N(4,1),
∴ PM=1,PM=4﹣1=3,
∴ PN=3PM;
② 由①知,如图,双曲线的解析式为y=![]() ,直线OA的解析式为y=x,
,直线OA的解析式为y=x,
∵ 点P的横坐标为n,
∴ P(n,n),
∵ PM//x轴,
∴ M(0,n),N(![]() ,n),
,n),
∵ PN≥3PM,
∴ PM=n,PN=![]() ﹣n,
﹣n,
∵ PN≥3PM,
∴![]() ﹣n≥3n,
﹣n≥3n,
∴ 0<n≤1.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.

(1)求反比例函数的表达式;
(2)若![]() 的面积为
的面积为![]() 的面积的2倍,求此直线的函数表达式.
的面积的2倍,求此直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABC中,AB=BC,以△ABC的边AB为直径作⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
ABC中,AB=BC,以△ABC的边AB为直径作⊙O,交AC于点D,过点D作DE⊥BC,垂足为点E.
(1)试证明DE是⊙O的切线;
(2)若⊙O的半径为5,AC=6![]() ,求此时DE的长.
,求此时DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办“创建全国文明城市”知识竞赛,计划购买甲、乙两种奖品共30件.其中甲种奖品每件30元,乙种奖品每件20元.
(1)如果购买甲、乙两种奖品共花费800元,那么这两种奖品分别购买了多少件?
(2)若购买乙种奖品的件数不超过甲种奖品件数的3倍,如何购买甲、乙两种奖品,使得总花费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过使用手机app购票,智能闸机、手持验票机验票的方式,能够大大缩短游客排队购票、验票的等待时间,且操作极其简单,已知某公园采用新的售票、验票方式后,平均每分钟接待游客的人数是原来的10倍,且接待5000名游客的入园时间比原来接待600名游客的入园时间还少5分钟,求该公园原来平均每分钟接待游客的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店经销A、B两种水果,A种水果进货单价比B种水果进货单价多2元,花50元购进A种水果的数量与花40元购进B种水果的数量相同.在销售过程中发现,A种水果每天销售量是![]() 与销售价x(元)满足关系式
与销售价x(元)满足关系式![]() ,B种水果,每天销售量
,B种水果,每天销售量![]() 与销售价x(元)满足
与销售价x(元)满足![]() = -x+14
= -x+14
(1)求A、B两种水果的单价.
(2)已知A种水果比B种水果的销售价高2元/千克,且每天A、B水果均有a千克坏掉.设B水果售价为t元/千克,每天两种水果的总利润为W元,求W与t的函数解析式,并求出当a的取值在什么范围内,水果店有可能不赔钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数![]() 的图像(记为抛物线
的图像(记为抛物线![]() )与y轴交于点C,与x轴分别交于点A、B,点A、B的横坐标分别记为
)与y轴交于点C,与x轴分别交于点A、B,点A、B的横坐标分别记为![]() ,
,![]() ,且
,且![]() .
.
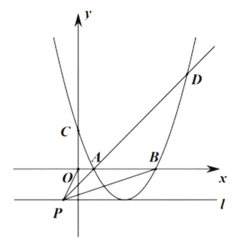
(1)若![]() ,
,![]() ,且过点
,且过点![]() ,求该二次函数的表达式;
,求该二次函数的表达式;
(2)若关于x的一元二次方程![]() 的判别式
的判别式![]() .求证:当
.求证:当![]() 时,二次函数
时,二次函数![]() 的图像与x轴没有交点.
的图像与x轴没有交点.
(3)若![]() ,点P的坐标为
,点P的坐标为![]() ,过点P作直线l垂直于y轴,且抛物线的
,过点P作直线l垂直于y轴,且抛物线的![]() 顶点在直线l上,连接OP、AP、BP,PA的延长线与抛物线
顶点在直线l上,连接OP、AP、BP,PA的延长线与抛物线![]() 交于点D,若
交于点D,若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
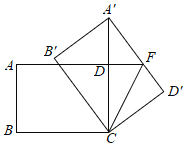
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 旋转,点
旋转,点![]() 、
、![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() 、
、![]() ,当
,当![]() 落在边
落在边![]() 的延长线上时,边
的延长线上时,边![]() 与边
与边![]() 的延长线交于点
的延长线交于点![]() ,联结
,联结![]() ,那么线段
,那么线段![]() 的长度为_________.
的长度为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com