
【题目】陕西省某甜瓜基地因“规模大、品质好、品牌亮”吸引了周边大批水果批发商订购,该基地对需要送货上门且购买量在![]() (含1000kg和3000kg)的客户制定了两种销售方案(客户只能选择其中一种方案),已知该基地甜瓜批发价随市场变化波动,设某天批发价为每千克m元.
(含1000kg和3000kg)的客户制定了两种销售方案(客户只能选择其中一种方案),已知该基地甜瓜批发价随市场变化波动,设某天批发价为每千克m元.
方案一:每千克![]() 元,免运费;
元,免运费;
方案二:每千克m元,客户需支付运费1200元.
(1)请分别写出这一天按方案一、方案二购买这种甜瓜的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)当购买量x在什么范围时,选择方案二比方案一付款少;
(3)已知5月某天批发价为每千克8元,某水果批发商计划用25000元在这一天购买尽可能多的这种甜瓜并需要送货上门,那么他在这两种方案中,应选择哪一种方案?
科目:初中数学 来源: 题型:
【题目】某校举办“创建全国文明城市”知识竞赛,计划购买甲、乙两种奖品共30件.其中甲种奖品每件30元,乙种奖品每件20元.
(1)如果购买甲、乙两种奖品共花费800元,那么这两种奖品分别购买了多少件?
(2)若购买乙种奖品的件数不超过甲种奖品件数的3倍,如何购买甲、乙两种奖品,使得总花费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
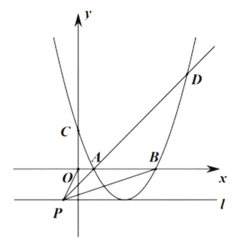
【题目】如图所示,二次函数![]() 的图像(记为抛物线
的图像(记为抛物线![]() )与y轴交于点C,与x轴分别交于点A、B,点A、B的横坐标分别记为
)与y轴交于点C,与x轴分别交于点A、B,点A、B的横坐标分别记为![]() ,
,![]() ,且
,且![]() .
.
(1)若![]() ,
,![]() ,且过点
,且过点![]() ,求该二次函数的表达式;
,求该二次函数的表达式;
(2)若关于x的一元二次方程![]() 的判别式
的判别式![]() .求证:当
.求证:当![]() 时,二次函数
时,二次函数![]() 的图像与x轴没有交点.
的图像与x轴没有交点.
(3)若![]() ,点P的坐标为
,点P的坐标为![]() ,过点P作直线l垂直于y轴,且抛物线的
,过点P作直线l垂直于y轴,且抛物线的![]() 顶点在直线l上,连接OP、AP、BP,PA的延长线与抛物线
顶点在直线l上,连接OP、AP、BP,PA的延长线与抛物线![]() 交于点D,若
交于点D,若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
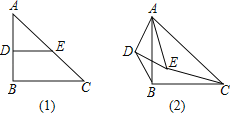
【题目】如图1,在![]() 中,
中,![]() ,点D、E分别是边
,点D、E分别是边![]() 的中点,连接
的中点,连接![]() ,将
,将![]() 绕点A按顺时针方向旋转,记旋转角为
绕点A按顺时针方向旋转,记旋转角为![]() ,
,![]() 、
、![]() 所在直线相交所成的锐角为
所在直线相交所成的锐角为![]() .
.
(1)问题发现
当![]() 时,
时,![]() ________;
________;![]() ________°.
________°.
(2)拓展探究
试判断:当![]() 时,
时,![]() 和
和![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)在![]() 旋转过程中,当
旋转过程中,当![]() 时,直接写出此时
时,直接写出此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批A、B两型号节能灯,已知2只A型节能灯和3只B型节能灯共需31元;1只A型节能灯和2只B型节能灯共需19元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元?
(2)学校准备购进这两种型号的节能灯共100只,并且A型节能灯的数量不多于B型节能灯数量的2倍,请设计出最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
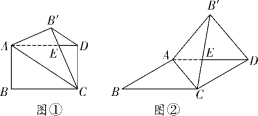
【题目】实践操作
如图①,将矩形纸片![]() 沿对角线
沿对角线![]() 翻折,使点
翻折,使点![]() 落在矩形
落在矩形![]() 所在平面内,
所在平面内,![]() 和
和![]() 相交于点E,连接
相交于点E,连接![]() .
.
解决问题
(1)在图①中,
①![]() 和
和![]() 的位置关系为________;
的位置关系为________;
②将![]() 剪下后展开,得到的图形是________;
剪下后展开,得到的图形是________;
(2)若图①中的矩形变为平行四边形时(![]() ),如图②所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明,若不成立,请说明理由;
),如图②所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明,若不成立,请说明理由;
拓展应用
(3)在图②中,若![]() ,当
,当![]() 恰好为直角三角形时,求
恰好为直角三角形时,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
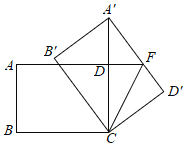
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 旋转,点
旋转,点![]() 、
、![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() 、
、![]() ,当
,当![]() 落在边
落在边![]() 的延长线上时,边
的延长线上时,边![]() 与边
与边![]() 的延长线交于点
的延长线交于点![]() ,联结
,联结![]() ,那么线段
,那么线段![]() 的长度为_________.
的长度为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
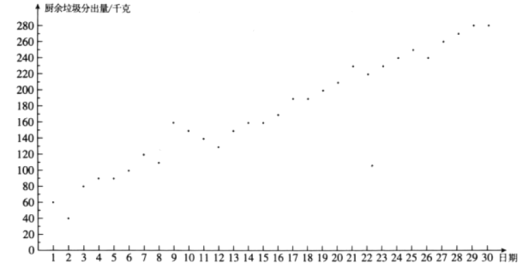
【题目】小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
![]() .小云所住小区5月1日至30日的厨余垃圾分出量统计图:
.小云所住小区5月1日至30日的厨余垃圾分出量统计图:
![]() .小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
时段 | 1日至10日 | 11日至20日 | 21日至30日 |
平均数 | 100 | 170 | 250 |
(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为 (结果取整数)
(2)已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的 倍(结果保留小数点后一位);
(3)记该小区5月1日至10日的厨余垃圾分出量的方差为![]() 5月11日至20日的厨余垃圾分出量的方差为
5月11日至20日的厨余垃圾分出量的方差为![]() ,5月21日至30日的厨余垃圾分出量的方差为
,5月21日至30日的厨余垃圾分出量的方差为![]() .直接写出
.直接写出![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】县政府计划建设一项水利工程,工程需要运送的土石方总量为![]() (单位:
(单位:![]() ),某运输公司承担了运送土石方的任务.
),某运输公司承担了运送土石方的任务.
(1)运输公司平均运输速度v(单位:![]() 天)与完成运输所需时间t(单位:天)之间具有怎样的函数关系?
天)与完成运输所需时间t(单位:天)之间具有怎样的函数关系?
(2)这个运输公司共有80辆卡车,每天可运输土石方为![]() (单位:
(单位:![]() ),公司完成全部运输任务需要多长时间?
),公司完成全部运输任务需要多长时间?
(3)当公司以问题(2)中的速度工作了30天后,由于工程进度的需要,剩下的运输任务必须在20天内完成,则运输公司至少要增加多少辆卡车?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com