
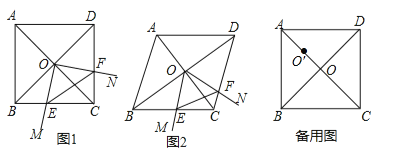
【题目】(12分)菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是 ;
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且![]() 时,直接写出线段CE的长.
时,直接写出线段CE的长.
【答案】(1)△OEF是等腰直角三角形;(2)△OEF是等边三角形;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)先证四边形ABCD是正方形,得出∠EBO=∠FCO=45°,OB=OC,得出∠BOE=∠COF,进一步得到△BOE≌△COF,从而得到结论;
(2)过O点作OG⊥BC于G,作OH⊥CD于H,根据菱形的性质可得CA平分∠BCD,∠ABC+BCD=180°,求得OG=OH,∠BCD=120°,∠GOH=∠EOF=60°,进一步得出∠EOG=∠FOH,得出△EOG≌△FOH,从而得到结论;
(3)过O点作OG⊥BC于G,作OH⊥CD于H,先求得四边形O′GCH是正方形,从而求得GC=O′G=3,∠GO′H=90°,得到△EO′G ≌△FO′H全等,得到△O′EF是等腰直角三角形,根据已知求得等腰直角三角形的直角边O′E的长,然后根据勾股定理求得EG,即可求得CE的长.
试题解析:(1)△OEF是等腰直角三角形;如图1,∵菱形ABCD中,∠ABC=90°,∴四边形ABCD是正方形,∴OB=OC,∠BOC=90°,∠BCD=90°,∠EBO=∠FCO=45°,∴∠BOE+∠COE=90°,∵∠MON+∠BCD=180°,∴∠MON=90°,∴∠COF+∠COE=90°,∴∠BOE=∠COF,在△BOE与△COF中,∵∠BOE=∠COF,OB=OC,∠EBO=∠FCO,∴△BOE≌△COF(ASA),∴OE=OF,∴△OEF是等腰直角三角形;
(2)△OEF是等边三角形;如图2,过O点作OG⊥BC于G,作OH⊥CD于H,∴∠OGE=∠OGC=∠OHC=90°,∵四边形ABCD是菱形,∴CA平分∠BCD,∠ABC+BCD=180°,∴OG=OH,∠BCD=180°﹣60°=120°,∵∠GOH+∠OGC+∠BCD+∠OHC=360°,∴∠GOH+∠BCD=180°,∴∠MON+∠BCD=180°,∴∠GOH=∠EOF=60°,∵∠GOH=∠GOF+∠FOH,∠EOF=∠GOF+∠EOG,∴∠EOG=∠FOH,在△EOG与△FOH中,∵∠EOG=∠FOH,OG=OH,∠EGO=∠FHO,∴△EOG≌△FOH(ASA),∴OE=OF,∴△OEF是等边三角形;
(3)如图3,∵菱形ABCD中,∠ABC=90°,∴四边形ABCD是正方形,∴![]() ,过O点作O′G⊥BC于G,作O′H⊥CD于H,∴∠O′GC=∠O′HC=∠BCD=90°,∴四边形O′GCH是矩形,∴O′G∥AB,O′H∥AD,∴
,过O点作O′G⊥BC于G,作O′H⊥CD于H,∴∠O′GC=∠O′HC=∠BCD=90°,∴四边形O′GCH是矩形,∴O′G∥AB,O′H∥AD,∴![]() ,∵AB=BC=CD=AD=4,∴O′G=O′H=3,∴四边形O′GCH是正方形,∴GC=O′G=3,∠GO′H=90°,∵∠MO′N+∠BCD=180°,∴∠EO′F=90°,∴∠EO′F=∠GO′H=90°,∵∠GO′H=∠GO′F+∠FO′H,∠EO′F=∠GO′F+∠EO′G,∴∠EO′G=∠FO′H,在△EO′G与△FO′H中,∵∠EO′G=∠FO′H,O′G= O′H,∠EG O′=∠FH O′,∴△EO′G≌△FO′H(ASA),∴O′E=O′F,∴△O′EF是等腰直角三角形;∵S正方形ABCD=4×4=16,
,∵AB=BC=CD=AD=4,∴O′G=O′H=3,∴四边形O′GCH是正方形,∴GC=O′G=3,∠GO′H=90°,∵∠MO′N+∠BCD=180°,∴∠EO′F=90°,∴∠EO′F=∠GO′H=90°,∵∠GO′H=∠GO′F+∠FO′H,∠EO′F=∠GO′F+∠EO′G,∴∠EO′G=∠FO′H,在△EO′G与△FO′H中,∵∠EO′G=∠FO′H,O′G= O′H,∠EG O′=∠FH O′,∴△EO′G≌△FO′H(ASA),∴O′E=O′F,∴△O′EF是等腰直角三角形;∵S正方形ABCD=4×4=16,![]() ,∴S△O′EF=18,∵S△O′EF=
,∴S△O′EF=18,∵S△O′EF=![]() ,∴O′E=6,在RT△O′EG中,EG=
,∴O′E=6,在RT△O′EG中,EG=![]() =
=![]() =
=![]() ,∴CE=CG+EG=
,∴CE=CG+EG=![]() .根据对称性可知,当∠M′ON′旋转到如图所示位置时,CE′=E′G﹣CG=
.根据对称性可知,当∠M′ON′旋转到如图所示位置时,CE′=E′G﹣CG=![]() .
.
综上可得,线段CE的长为![]() 或
或![]() .
.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
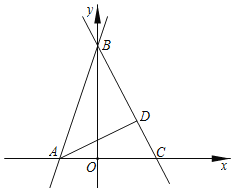
【题目】已知如图,直线AB交x轴于点A,交y轴于点B,AB=![]() ,tan∠BAO=3.
,tan∠BAO=3.
(1)求直线AB的解析式;
(2)直线y=kx+b经过点B交x轴交于点C,且∠ABC=45°,AD⊥BC于点D.动点P从点C出发,沿CB方向以每秒![]() 个单位长度的速度向终点B运动,运动时间为t,设△ADP的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围.
个单位长度的速度向终点B运动,运动时间为t,设△ADP的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围.
(3)在(2)的条件下,点P在线段BD上,点F在线段AB上,∠APC=∠FPB,连接AP,过点F作FG⊥AP于点G,交AD于点H,若DP=DH,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
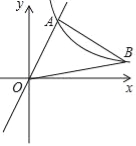
【题目】如图,在平面直角坐标系中,经过点A的双曲线y=![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为![]() ,∠AOB=∠OBA=45°,则k的值为 .
,∠AOB=∠OBA=45°,则k的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,BA=5,点D是边AC上的一动点,过点D作DE∥AB交边BC于点E,过点B作BF⊥BC交DE的延长线于点F,分别以DE,EF为对角线画矩形CDGE和矩形HEBF,则在D从A到C的运动过程中,当矩形CDGE和矩形HEBF的面积和最小时,AD的长度为______.
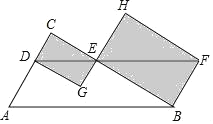
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装柜在销售中发现某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现,如果每件童装每降价4元,那么平均每天就可多售出8件,要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形 AOBC 中,AC∥OB,且 OB=6,AC=5,OA=4.
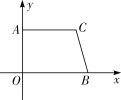
(1)求 B、C 两点的坐标;
(2)以 O、A、B、C 中的三点为顶点可组成哪几个不同的三角形?
(3)是否在边 AC 和 BC(含端点)上分别存在点 M 和点 N,使得△MON 的面积最大时,它的周长还最短?若存在,说明理由,并求出这时点 M、N 的坐标;若不存在,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com