
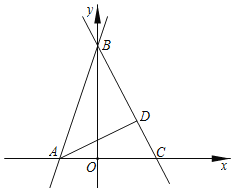
ЁОЬтФПЁПвбжЊШчЭМЃЌжБЯпABНЛxжсгкЕуAЃЌНЛyжсгкЕуBЃЌABЃН![]() ЃЌtanЁЯBAOЃН3ЃЎ
ЃЌtanЁЯBAOЃН3ЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ2ЃЉжБЯпyЃНkx+bОЙ§ЕуBНЛxжсНЛгкЕуCЃЌЧвЁЯABCЃН45ЁуЃЌADЁЭBCгкЕуDЃЎЖЏЕуPДгЕуCГіЗЂЃЌбиCBЗНЯђвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуBдЫЖЏЃЌдЫЖЏЪБМфЮЊtЃЌЩшЁїADPЕФУцЛ§ЮЊSЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЎ
ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуBдЫЖЏЃЌдЫЖЏЪБМфЮЊtЃЌЩшЁїADPЕФУцЛ§ЮЊSЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕуPдкЯпЖЮBDЩЯЃЌЕуFдкЯпЖЮABЩЯЃЌЁЯAPCЃНЁЯFPBЃЌСЌНгAPЃЌЙ§ЕуFзїFGЁЭAPгкЕуGЃЌНЛADгкЕуHЃЌШєDPЃНDHЃЌЧѓЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН3x+6ЃЛЃЈ2ЃЉЕБ0ЁмtЃМ1ЪБЃЌSЃН5Љ5xЃЌЕБ1ЃМtЁм3ЪБЃЌSЃН5xЉ5ЃЛЃЈ3ЃЉЕуPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩШ§НЧКЏЪ§КЭЙДЙЩЖЈРэПЩЧѓЕуAЃЌЕуBзјБъЃЌгУД§ЖЈЯЕЪ§ЗЈПЩЧѓНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуDзїEFЁЭACЃЌНЛACгкЕуFЃЌЙ§ЕуBзїBEЁЭEFЃЌДЙзуЮЊEЃЌгЩЁАAASЁБПЩжЄЁїBDEЁеЁїDAFЃЌПЩЕУDFЃНBEЃЌDEЃНAFЃЌПЩЧѓЕуDзјБъЃЌПЩЧѓBCНтЮіЪНЃЌгЩЙДЙЩЖЈРэПЩЧѓBCЕФГЄЃЌгЩУцЛ§ЙЋЪНПЩЧѓНтЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЙ§ЕуBзїBNЁЭABНЛAPбгГЄЯпгкNЃЌгЩЁАASAЁБПЩжЄЁїBPNЁеЁїBPFЃЌПЩЕУBNЃНBFЃЌPNЃНPFЃЌгЩЁАAASЁБПЩжЄЁїAHFЁеЁїBPNЃЌПЩЕУAFЃНBNЃЌPNЃНFHЃЌПЩЧѓЕуFзјБъЃЌгЩСНЕуОрРыЙЋЪНПЩЧѓBFЃН![]() ЃНBNЃЌЭЈЙ§жЄУїЁїMNPЁзЁїDAPЃЌПЩЕУ
ЃНBNЃЌЭЈЙ§жЄУїЁїMNPЁзЁїDAPЃЌПЩЕУ![]() ЃЌПЩЧѓPDЕФГЄЃЌгЩСНЕуОрРыЙЋЪНПЩЧѓЕуPзјБъЃЎ
ЃЌПЩЧѓPDЕФГЄЃЌгЩСНЕуОрРыЙЋЪНПЩЧѓЕуPзјБъЃЎ
НтЃКЃЈ1ЃЉЁпtanЁЯBAOЃН3ЃН![]() ЃЌ
ЃЌ
ЁрBOЃН3AOЃЌ
ЁпAB2ЃНAO2+BO2ЃН40ЃЌ
ЁрAOЃН2ЃЌBOЃН6ЃЌ
ЁрЕуAЃЈЉ2ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌ6ЃЉ
ЩшжБЯпABНтЮіЪНЮЊЃКyЃНkx+6ЃЌ
Ёр0ЃНЉ2k+6ЃЌ
ЁрkЃН3ЃЌ
ЁржБЯпABНтЮіЪНЮЊЃКyЃН3x+6ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуDзїEFЁЭACЃЌНЛACгкЕуFЃЌЙ§ЕуBзїBEЁЭEFЃЌДЙзуЮЊEЃЌ
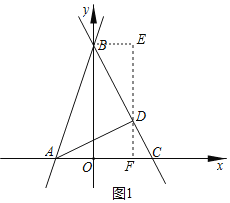
ЁрЫФБпаЮBEFOЪЧОиаЮЃЌ
ЁрBOЃНEFЃН6ЃЌOFЃНBEЃЌ
ЁпЁЯABCЃН45ЁуЃЌADЁЭBCЃЌ
ЁрЁЯABCЃНЁЯBADЃН45ЁуЃЌ
ЁрADЃНBDЃЌ
ЁпЁЯADBЃН90ЁуЃНЁЯAFDЃЌ
ЁрЁЯBDE+ЁЯADFЃН90ЁуЃЌЁЯADF+ЁЯDAFЃН90ЁуЃЌ
ЁрЁЯBDEЃНЁЯDAFЃЌЧвBDЃНADЃЌЁЯEЃНЁЯAFDЃН90ЁуЃЌ
ЁрЁїBDEЁеЁїDAFЃЈAASЃЉ
ЁрDFЃНBEЃЌDEЃНAFЃЌ
ЁпEFЃНED+DFЃНAO+OF+OFЃН2+2OFЃН6
ЁрOFЃН2ЃЌ
ЁрЕуDзјБъЃЈ2ЃЌ2ЃЉЃЌ
ЩшBCНтЮіЪНЮЊЃКyЃНax+6ЃЌ
Ёр2ЃН2a+6ЃЌ
ЁрaЃНЉ2ЃЌ
ЁржБЯпBCНтЮіЪНЮЊЃКyЃНЉ2x+6ЃЌ
ЁрЕБyЃН0ЪБЃЌxЃН3ЃЌ
ЁрЕуCЃЈ3ЃЌ0ЃЉЃЌ
ЁрOCЃН3ЃЌ
ЁрBCЃН![]() ЃН3
ЃН3![]() ЃЌ
ЃЌ
ЁпABЃН2![]() ЃЌЧвЁЯABCЃН45ЁуЃЌADЁЭBCЃЌ
ЃЌЧвЁЯABCЃН45ЁуЃЌADЁЭBCЃЌ
ЁрADЃНBDЃН2![]() ЃЌ
ЃЌ
ЁрCDЃН![]() ЃЌ
ЃЌ
ЕБ0ЁмtЃМ1ЪБЃЌSЃН![]() ЁС2
ЁС2![]() ЁСЃЈ
ЁСЃЈ![]() Љ
Љ![]() xЃЉЃН5Љ5xЃЌ
xЃЉЃН5Љ5xЃЌ
ЕБ1ЃМtЁм3ЪБЃЌSЃН![]() ЁС2
ЁС2![]() ЁСЃЈ
ЁСЃЈ![]() xЉ
xЉ![]() ЃЉЃН5xЉ5ЃЛ
ЃЉЃН5xЉ5ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЙ§ЕуBзїBNЁЭABНЛAPбгГЄЯпгкNЃЌЙ§ЕуNзїMNЁЭBCгкMЃЌ
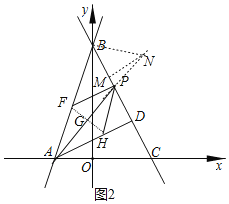
ЁпADЃНBDЃЌDHЃНPDЃЌ
ЁрAHЃНBPЃЌ
ЁпBNЁЭABЃЌЁЯABCЃН45ЁуЃЌ
ЁрЁЯABCЃНЁЯNBPЃН45ЁуЃЌЧвЁЯAPCЃНЁЯBPNЃНЁЯBPFЃЌBPЃНBPЃЌ
ЁрЁїBPNЁеЁїBPFЃЈASAЃЉ
ЁрBNЃНBFЃЌPNЃНPFЃЌ
ЁпFHЁЭAPЃЌ
ЁрЁЯAGFЃНЁЯABNЃН90ЁуЃЌ
ЁрЁЯFAG+ЁЯAFGЃН90ЁуЃЌЁЯFAG+ЁЯNЃН90ЁуЃЌ
ЁрЁЯAFGЃНЁЯNЃЌЧвЁЯBADЃНЁЯPBNЃН45ЁуЃЌAHЃНBPЃЌ
ЁрЁїAHFЁеЁїBPNЃЈAASЃЉ
ЁрAFЃНBNЃЌPNЃНFHЃЌ
ЁрBFЃНAFЃЌFHЃНFPЃЌ
ЁрЕуFЪЧABжаЕуЃЌ
ЁрЕуFзјБъЃЈЉ1ЃЌ3ЃЉ
ЁрBFЃН![]() ЃНBNЃЌ
ЃНBNЃЌ
ЁпЁЯNBMЃН45ЁуЃЌ
ЁрBMЃНMNЃН![]() ЃЌ
ЃЌ
ЁрMDЃНBDЉBMЃН![]() ЃЌ
ЃЌ
ЁпMNЁЭBCЃЌADЁЭBCЃЌ
ЁрADЁЮMNЃЌ
ЁрЁїMNPЁзЁїDAPЃЌ
Ёр![]()
Ёр![]() ЃЌЧвMP+PDЃН
ЃЌЧвMP+PDЃН![]()
ЁрPDЃН![]()
ЩшЕуPЃЈxЃЌЉ2x+6ЃЉЃЌ
ЁрЃЈxЉ2ЃЉ2+ЃЈЉ2x+6Љ2ЃЉ2ЃН![]() ЃЌ
ЃЌ
ЁрxЃН![]() ЃЌxЃН
ЃЌxЃН![]() ЃЈВЛКЯЬтвтЩсШЅЃЉ
ЃЈВЛКЯЬтвтЩсШЅЃЉ
ЁрЕуPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФПкДќРязАгаШєИЩИіжЪЕиЯрЭЌЕФКьЧђЃЌЮЊСЫЙРМЦДќжаКьЧђЕФЪ§СПЃЌФГбЇЯАаЁзщзіСЫУўЧђЪдбщЃЌЫћУЧНЋ30ИігыКьЧђДѓаЁаЮзДЭъШЋЯрЭЌЕФАзЧђзАШыДќжаЃЌНСдШКѓДгжаЫцЛњУўГі1ИіЧђВЂМЧЯТбеЩЋЃЌдйАбЫќЗХЛиДќжаЃЌЖрДЮжиИДУўЧђЃЎЯТБэЪЧЖрДЮУўЧђЪдбщЛузмКѓЭГМЦЕФЪ§ОнЃК
УўЧђЕФДЮЪ§ | 150 | 200 | 500 | 900 | 1 000 | 1 200 |
УўЕНАзЧђЕФЦЕЪ§ | 51 | 64 | 156 | 275 | 303 | 361 |
УўЕНАзЧђЕФЦЕТЪ | 0.320 | 0.312 | 0.306 | 0.303 | 0.302 | 0.301 |
(1)ЧыЙРМЦЃКЕБУўЧђЕФДЮЪ§КмДѓЪБЃЌУўЕНАзЧђЕФЦЕТЪНЋЛсНгНќ______ЃЛМйШчФуШЅУўвЛДЮЃЌФуУўЕНКьЧђЕФИХТЪЪЧ______ЃЛ(ОЋШЗЕН0.1)
(2)ЪдЙРМЦПкДќжаКьЧђгаЖрЩйИіЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЫФБпаЮABGCФкНггкЁбOЃЌGAЦНЗжЁЯBGCЃЎ
ЃЈ1ЃЉЧѓжЄЃКABЃНACЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуAзїADЁЮBGНЛCGгкЕуDЃЌСЌНгBDНЛЯпЖЮAGгкЕуWЃЌШєЁЯBAG+ЁЯCADЃНЁЯAWBЃЌЧѓжЄЃКBDЃНBGЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєCDЃН5ЃЌBDЃН16ЃЌЧѓWGЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГПЮЭтЛюЖЏаЁзщзМБИЮЇНЈвЛИіОиаЮЩњЮяУчЦдЃЌЦфжавЛБпППЧНЃЌСэШ§БпгУГЄЮЊ![]() УзЕФРщАЪЮЇГЩЃЌвбжЊЧНГЄЮЊ
УзЕФРщАЪЮЇГЩЃЌвбжЊЧНГЄЮЊ![]() УзЃЈШчЭМЫљЪОЃЉЃЌЩшетИіУчЦдДЙжБгкЧНЕФвЛБпЕФГЄЮЊ
УзЃЈШчЭМЫљЪОЃЉЃЌЩшетИіУчЦдДЙжБгкЧНЕФвЛБпЕФГЄЮЊ![]() Уз.
Уз.

ЃЈ1ЃЉДЙжБгкЧНЕФвЛБпБпЕФГЄЮЊЖрЩйУзЪБЃЌетИіУчЦдЕФУцЛ§зюДѓЃЌВЂЧѓГіетИізюДѓжЕЃЛ
ЃЈ2ЃЉЕБетИіУчЦдЕФУцЛ§ВЛаЁгк![]() ЦНЗНУзЪБЃЌЪдНсКЯКЏЪ§ЭМЯѓЃЌжБНгаДГіЕФШЁжЕЗЖЮЇ.
ЦНЗНУзЪБЃЌЪдНсКЯКЏЪ§ЭМЯѓЃЌжБНгаДГіЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШбќЁїABCжаЃЌABЃНACЃЌtanЁЯCABЃН![]() ЃЌADЃНABЃЌAHЁЭBDгкЕуHЃЌСЌНгCDНЛAHгкЕуEЃЌСЌНгBEЃЌBEЃН
ЃЌADЃНABЃЌAHЁЭBDгкЕуHЃЌСЌНгCDНЛAHгкЕуEЃЌСЌНгBEЃЌBEЃН![]() ЃЌдђBDЕФГЄЮЊ_____ЃЎ
ЃЌдђBDЕФГЄЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНx2Љ2xЉ3гыxжсНЛгкЕуAЃЈ1ЃЌ0ЃЉЃЌЕуBЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЌЕуDЪЧИУХзЮяЯпЕФЖЅЕуЃЌСЌНгADЃЌBDЃЎ
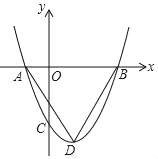
ЃЈ1ЃЉЧѓЁїABDЕФУцЛ§ЃЛ
ЃЈ2ЃЉЕуPЪЧХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЧвЕуPдкxжсЩЯЗНЃЌШєЁїABPЕФУцЛ§ЪЧЁїABDУцЛ§ЕФ![]() ЃЌЧѓЕуPЕФзјБъЃЎ
ЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУЪЪЕБЕФЗНЗЈНтвЛдЊЖўДЮЗНГЬ
ЃЈ1ЃЉЃЈxЉ1ЃЉ2ЃН4
ЃЈ2ЃЉЃЈxЉ3ЃЉ2ЃН2xЃЈ3ЉxЃЉ
ЃЈ3ЃЉ2x2+5xЉ1ЃН0
ЃЈ4ЃЉЃЈxЉ1ЃЉЃЈxЉ3ЃЉЃН8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌBDЃН2ADЃЌEЁЂFЁЂGЗжБ№ЪЧOCЁЂODЁЂABЕФжаЕуЃЌЯТСаНсТлЃКЂйBEЁЭACЃЛЂкЫФБпаЮBEFGЪЧЦНааЫФБпаЮЃЛЂлЁїEFGЁеЁїGBEЃЛЂмEGЃНEFЃЌЦфжае§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
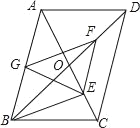
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
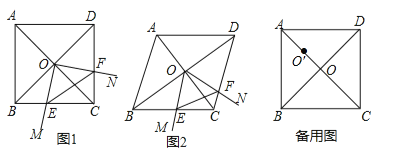
ЁОЬтФПЁПЃЈ12ЗжЃЉСтаЮABCDжаЃЌСНЬѕЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌЁЯMON+ЁЯBCD=180ЁуЃЌЁЯMONШЦЕуOа§зЊЃЌЩфЯпOMНЛБпBCгкЕуEЃЌЩфЯпONНЛБпDCгкЕуFЃЌСЌНгEFЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЁЯABC=90ЁуЪБЃЌЁїOEFЕФаЮзДЪЧ ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЁЯABC=60ЁуЪБЃЌЧыХаЖЯЁїOEFЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌНЋЁЯMONЕФЖЅЕувЦЕНAOЕФжаЕуOЁфДІЃЌЁЯMOЁфNШЦЕуOЁфа§зЊЃЌШдТњзуЁЯMOЁфN+ЁЯBCD=180ЁуЃЌЩфЯпOЁфMНЛжБЯпBCгкЕуEЃЌЩфЯпOЁфNНЛжБЯпCDгкЕуFЃЌЕБBC=4ЃЌЧв![]() ЪБЃЌжБНгаДГіЯпЖЮCEЕФГЄЃЎ
ЪБЃЌжБНгаДГіЯпЖЮCEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com