
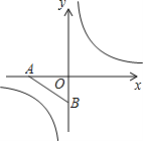
【题目】在平面直角坐标系中,已知点A、B的坐标分别为(-![]() ,0)、(0,-1),把点A绕坐标原点O顺时针旋转135°得点C,若点C在反比例函数y=
,0)、(0,-1),把点A绕坐标原点O顺时针旋转135°得点C,若点C在反比例函数y=![]() 的图象上.
的图象上.
(1)求反比例函数的表达式;
(2)若点D在y轴上,点E在反比例函数y=![]() 的图象上,且以点A、B、D、E为顶点的四边形是平行四边形.请画出满足题意的示意图并在示意图的下方直接写出相应的点D、E的坐标.
的图象上,且以点A、B、D、E为顶点的四边形是平行四边形.请画出满足题意的示意图并在示意图的下方直接写出相应的点D、E的坐标.
【答案】(1)y=![]() ;(2)示意图见解析,E(-
;(2)示意图见解析,E(-![]() ,-
,-![]() ),D(0,-1-
),D(0,-1-![]() )或E(-
)或E(-![]() ,-
,-![]() ),D(0,-1+
),D(0,-1+![]() )或E
)或E 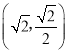 , D
, D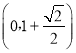
【解析】
(1)根据旋转和直角三角形的边角关系可以求出点C的坐标,进而确定反比例函数的关系式;
(2)分两种情况进行讨论解答,①点E在第三象限,由题意可得E的横坐标与点A的相同,将A的横坐标代入反比例函数的关系式,可求出纵坐标,得到E的坐标,进而得到AE的长,也是BD的长,因此D在B的上方和下方,即可求出点D的坐标,②点E在第一象限,由三角形全等,得到E的横坐标,代入求出纵坐标,确定E的坐标,进而求出点D的坐标.
(1)由旋转得:OC=OA=![]() ,∠AOC=135°,
,∠AOC=135°,
过点C作CM⊥y轴,垂足为M,则∠COM=135°-90°=45°,
在Rt△OMC中,∠COM=45°,OC=![]() ,
,
∴OM=CM=1,
∴点C(1,1),代入y=![]() 得:k=1,
得:k=1,
∴反比例函数的关系式为:y=![]() ,
,
答:反比例函数的关系式为:y=![]()
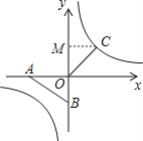
(2)①当点E在第三象限反比例函数的图象上,如图1,图2,
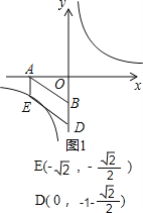
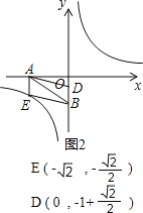
∵点D在y轴上,AEDB是平行四边形,
∴AE∥DB,AE=BD,AE⊥OA,
当x=-![]() 时,y=
时,y=![]() =-
=-![]() ,
,
∴E(-![]() ,-
,-![]() )
)
∵B(0,-1),BD=AE=![]() ,
,
当点D在B的下方时,
∴D(0,-1-![]() )
)
当点D在B的上方时,
∴D(0,-1+![]() ),
),
②当点E在第一象限反比例函数的图象上时,如图3,
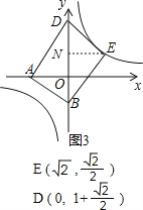
过点E作EN⊥y轴,垂足为N,
∵ABED是平行四边形,
∴AB=DE,AB=DE,
∴∠ABO=∠EDO,
∴△AOB≌△END (AAS),
∴EN=OA=![]() ,DN=OB=1,
,DN=OB=1,
当x=![]() 时,代入y=
时,代入y=![]() 得:y=
得:y=![]() ,
,
∴E(![]() ,
,![]() ),
),
∴ON=![]() ,OD=ON+DN=1+
,OD=ON+DN=1+![]() ,
,
∴D(0,1+![]() )
)


科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 坐标为
坐标为![]() .
.
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)画出将![]() 绕原点
绕原点![]() 逆时针旋转90°所得的
逆时针旋转90°所得的![]() ;
;
(3)![]() 与
与![]() 能组成轴对称图形吗?若能,请你画出所有的对称轴.
能组成轴对称图形吗?若能,请你画出所有的对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲校20名学生成绩的频数分布表和频数分布直方图如下:
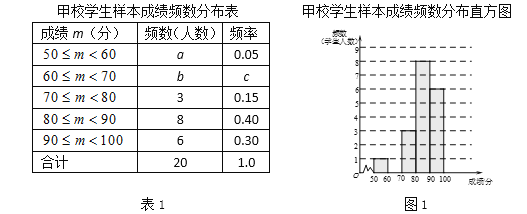
b.甲校成绩在![]() 的这一组的具体成绩是:
的这一组的具体成绩是:
87 88 88 88 89 89 89 89
c.甲、乙两校成绩的平均分、中位数、众数、方差如下:
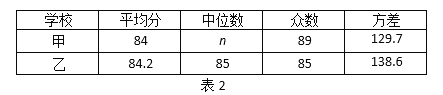
根据以上图表提供的信息,解答下列问题:
(1)表1中a = ;表2中的中位数n = ;
(2)补全图1甲校学生样本成绩频数分布直方图;
(3)在此次测试中,某学生的成绩是87分,在他所属学校排在前10名,由表中数据可知该学生是 校的学生(填“甲”或“乙”),理由是 ;
(4)假设甲校200名学生都参加此次测试,若成绩80分及以上为优秀,估计成绩优秀的学生人数为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
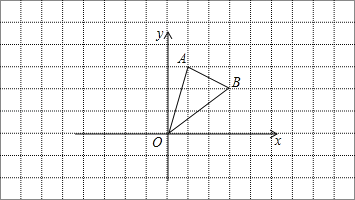
【题目】如图,在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)以原点O为对称中心,画出△ AOB与关于原点对称的△ A2 O B2;
(4)以原点O为旋转中心,画出把△AOB顺时针旋转90°的图形△A3 O B3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的有( )
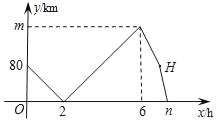
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
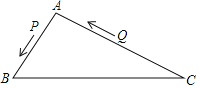
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t.
⑴用含t的代数式表示:AP= ,AQ= .
⑵当以A,P,Q为顶点的三角形与△ABC相似时,求运动时间是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com