
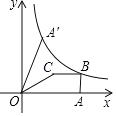
【题目】如图,平面直角坐标系xOy中,四边形OABC的边OA在x轴正半轴上,BC∥x轴,∠OAB=90°,点C(3,2),连接OC.以OC为对称轴将OA翻折到OA′,反比例函数y=![]() 的图象恰好经过点A′、B,则k的值是( )
的图象恰好经过点A′、B,则k的值是( )
A. 9B. ![]() C.
C. ![]() D. 3
D. 3![]()
【答案】C
【解析】
设B(![]() ,2),由翻折知OC垂直平分AA′,A′G=2EF,AG=2AF,由勾股定理得OC=
,2),由翻折知OC垂直平分AA′,A′G=2EF,AG=2AF,由勾股定理得OC=![]() ,根据相似三角形或锐角三角函数可求得A′(
,根据相似三角形或锐角三角函数可求得A′(![]() ,
,![]() ),根据反比例函数性质k=xy建立方程求k.
),根据反比例函数性质k=xy建立方程求k.
如图,过点C作CD⊥x轴于D,过点A′作A′G⊥x轴于G,连接AA′交射线OC于E,过E作EF⊥x轴于F,

设B(![]() ,2),
,2),
在Rt△OCD中,OD=3,CD=2,∠ODC=90°,
∴OC=![]() =
=![]() ,
,
由翻折得,AA′⊥OC,A′E=AE,
∴sin∠COD=![]() ,
,
∴AE=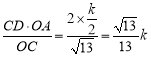 ,
,
∵∠OAE+∠AOE=90°,∠OCD+∠AOE=90°,
∴∠OAE=∠OCD,
∴sin∠OAE=![]() =sin∠OCD,
=sin∠OCD,
∴EF=![]() ,
,
∵cos∠OAE=![]() =cos∠OCD,
=cos∠OCD,
∴![]() ,
,
∵EF⊥x轴,A′G⊥x轴,
∴EF∥A′G,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴A′(![]() ,
,![]() ),
),
∴![]() ,
,
∵k≠0,
∴![]() ,
,
故选:C.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
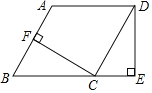
【题目】如图,在ABCD中,CF⊥AB于点F,过点D作DE⊥BC的延长线于点E,且CF=DE.
(1)求证:△BFC≌△CED;
(2)若∠B=60°,AF=5,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校文体艺术节期间,举办“爱我云南,唱我云南”文艺晚会.每个班推荐一个节目参加晩会表演,参加晚会表演的节目均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,明明根据获奖情况绘制岀如图所示的两幅统计图.请你根据图中所给信息解答下列问题.
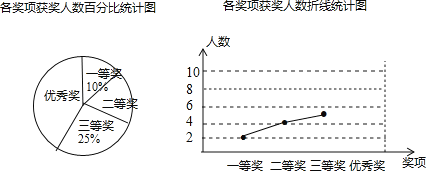
(1)二等奖的获奖人数所占的百分比是 ;
(2)在此次比赛中,一共有多少同学参赛?请将折线统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
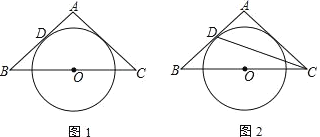
【题目】如图1,△ABC是等腰三角形,O是底边BC中点,腰AB与⊙O相切于点D
(1)求证:AC是⊙O的切线;
(2)如图2,连接CD,若tan∠BCD=![]() ,⊙O的半径为
,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果公司新购进10000千克柑橘,每千克柑橘的成本为9元. 柑橘在运输、存储过程中会有损坏,销售人员从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录如下:
柑橘总重量n/千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
损坏柑橘重量m/千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.54 |
柑橘损坏的频率 | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
根据以上数据,估计柑橘损坏的概率为 (结果保留小数点后一位);由此可知,去掉损坏的柑橘后,水果公司为了不亏本,完好柑橘每千克的售价至少为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
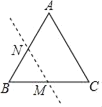
【题目】如图,在等边△ABC中,AB=4cm,点M为边BC的中点,点N为边AB上的任意一点(不与点A,B重合).若点B关于直线MN的对称点B'恰好落在等边△ABC的边上,则BN的长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
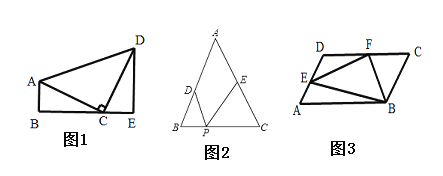
【题目】(问题引入)
如图(1),在![]() 中,
中,![]() ,
,![]() ,过
,过![]() 作则
作则![]() 交
交![]() 延长线于点
延长线于点![]() ,则易得
,则易得![]()
(直接应用)
如图,已知等边![]() 的边长为
的边长为![]() ,点
,点![]() ,
, ![]() 分别在边
分别在边![]() ,
, ![]() 上,
上, ![]() ,
, ![]() 为
为![]() 中点,
中点,![]() 为当
为当![]() 上一动点,当
上一动点,当![]() 在何处时,
在何处时,![]() 与
与![]() 相似,求
相似,求![]() 的值.
的值.
(拓展应用)
已知在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 长.
长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com