
【题目】如图1,△ABC是等腰三角形,O是底边BC中点,腰AB与⊙O相切于点D
(1)求证:AC是⊙O的切线;
(2)如图2,连接CD,若tan∠BCD=![]() ,⊙O的半径为
,⊙O的半径为![]() ,求BC的长.
,求BC的长.
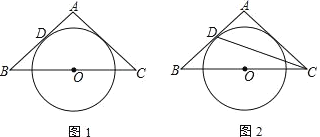
【答案】(1)证明见解析;(2)BC=6.
【解析】
(1)连接OD,作OF⊥AC于F,如图,利用等腰三角形的性质得AO⊥BC,AO平分∠BAC,再根据切线的性质得OD⊥AB,然后利用角平分线的性质得到OF=OD,从而根据切线的判定定理得到结论;
(2)过D作DF⊥BC于F,连接OD,根据三角函数的定义得到![]() ,设DF=
,设DF=![]() a,OF=x,则CF=4a,OC=4a-x根据相似三角形的性质得到
a,OF=x,则CF=4a,OC=4a-x根据相似三角形的性质得到![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
(1)证明:连接OD,OA,作OF⊥AC于F,如图,
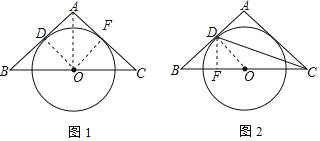
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO⊥BC,AO平分∠BAC,
∵AB与⊙O相切于点D,
∴OD⊥AB,
而OF⊥AC,
∴OF=OD,
∴AC是⊙O的切线;
(2)过D作DF⊥BC于F,连接OD,
∵tan∠BCD=![]() ,
,
∴![]() ,
,
设DF=![]() a,OF=x,则CF=4a,OC=4a﹣x,
a,OF=x,则CF=4a,OC=4a﹣x,
∵O是底边BC中点,
∴OB=OC=4a﹣x,
∴BF=OB﹣OF=4a﹣2x,
∵OD⊥AB,
∴∠BDO=90°,
∴∠BDF+∠FDO=90°,
∵DF⊥BC,
∴∠DFB=∠OFD=90°,∠FDO+∠DOF=90°,
∴∠BDF=∠DOF,
∴△DFO∽△BFD,
∴![]() ,
,
∴![]() ,
,
解得:x1=x2=a,
∵⊙O的半径为![]() ,
,
∴OD=![]() ,
,
∵DF2+FO2=DO2,
∴(![]() x)2+x2=(
x)2+x2=(![]() )2,
)2,
∴x1=x2=a=1,
∴OC=4a﹣x=3,
∴BC=2OC=6.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
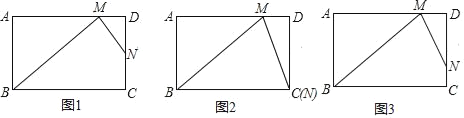
【题目】已知矩形ABCD,作∠ABC的平分线交AD边于点M,作∠BMD的平分线交CD边于点N.
(1)若N为CD的中点,如图1,求证:BM=AD+DM;
(2)若N与C点重合,如图2,求tan∠MCD的值;
(3)若![]() ,AB=6,如图3,求BC的长.
,AB=6,如图3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(–1,2),与x轴的一个交点A在点(–3,0)和(–2,0)之间,其部分图象如下图,则以下结论:①b2–4ac<0;②a+b+c<0;③c–a=2;④方程ax2+bx+c–2=0有两个相等的实数根.其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
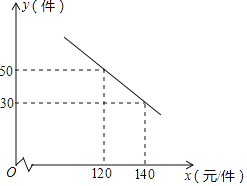
【题目】某商场购进一种每件价格为90元的新商品,在商场试销时发现:销售单价![]() 元
元![]() 件
件![]() 与每天销售量
与每天销售量![]() 件
件![]() 之间满足如图所示的关系.
之间满足如图所示的关系.
![]() 求出y与x之间的函数关系式;
求出y与x之间的函数关系式;
![]() 写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC与BD相交于点O,AB=4,BD=4![]() ,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )
,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )

A. 4B. 2![]() C. 2
C. 2![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年足球亚洲杯正在阿联酋进行,这项起源于我国“蹴鞠”的运动项目近年来在我国中小学校园得到大力推广,某次校园足球比赛规定:胜一场得3分,平一场得1分,负一场得0分,某足球队共进行了8场比赛,得了12分,该队获胜的场数有几种可能( )
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解了解节能减排、垃圾分类等知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查调查,调查结果分为“非常了解“、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制出以下两幅不完整的统计图,请根据统计图回答下列问题:
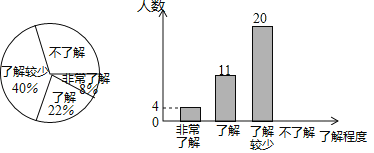
(1)本次调查的学生共有 人,估计该校2000名学生中“不了解”的人数约有 人.
(2)“非常了解”的4人中有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图和列表的方法,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A. 4 B. 6 C. 8 D. 不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com