
【题目】某校为了了解了解节能减排、垃圾分类等知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查调查,调查结果分为“非常了解“、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制出以下两幅不完整的统计图,请根据统计图回答下列问题:
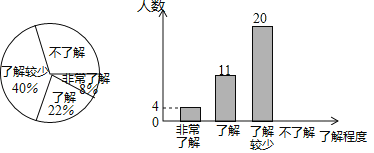
(1)本次调查的学生共有 人,估计该校2000名学生中“不了解”的人数约有 人.
(2)“非常了解”的4人中有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图和列表的方法,求恰好抽到2名男生的概率.
【答案】(1)50,600;(2)P(恰好抽到2名男生)=![]() .
.
【解析】(1)由“非常了解”的人数及其所占百分比求得总人数,继而由各了解程度的人数之和等于总人数求得“不了解”的人数,用总人数乘以样本中“不了解”人数所占比例可得;
(2)分别用树状图和列表两种方法表示出所有等可能结果,从中找到恰好抽到2名男生的结果数,利用概率公式计算可得.
(1)本次调查的学生总人数为4÷8%=50人,
则不了解的学生人数为50﹣(4+11+20)=15人,
∴估计该校2000名学生中“不了解”的人数约有2000×![]() =600人,
=600人,
故答案为:50、600;
(2)画树状图如下:
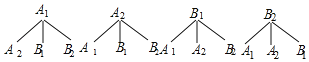
共有12种可能的结果,恰好抽到2名男生的结果有2个,
∴P(恰好抽到2名男生)=![]() .
.
列表如下:
A1 | A2 | B1 | B2 | |
A1 | (A2,A1) | (B1,A1) | (B2,A1) | |
A2 | (A1,A2) | (B1,A2) | (B2,A2) | |
B1 | (A1,B1) | (A2,B1) | (B2,B1) | |
B2 | (A1,B2) | (A2,B2) | (B1,B2) |
由表可知共有12种可能的结果,恰好抽到2名男生的结果有2个,
∴P(恰好抽到2名男生)=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“滴滴”司机沈师傅从上午8:00~9:15在东西方向的江平大道上营运,共连续运载十批乘客.若规定向东为正,向西为负,沈师傅营运十批乘客里程如下:(单位:千米)+8,-6,+3,-6,+8,+4,-8,-4,+3,+3.
(1)将最后一批乘客送到目的地时,沈师傅距离第一批乘客出发地的东面还是西面?距离多少千米?
(2) 若汽车每千米耗油0.4升,则8:00~9:15汽车共耗油多少升?
(3)若“滴滴”的收费标准为:起步价8元(不超过3千米),超过3千米,超过部分每千米2元.则沈师傅在上午8:00~9:15一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如下数据:
轿车行驶的路程 s(km) | 0 | 10 | 20 | 30 | 40 | … |
油箱剩余油量 w(L) | 50 | 49.2 | 48.4 | 47.6 | 46.8 | … |
(1)该轿车油箱的容量为 L,行驶 120km 时,油箱剩余油量为 L;
(2)根据上表的数据,写出油箱剩余油量 w(L)与轿车行驶的路程 s(km)之间的表达式 ;
(3)某人将油箱加满后,驾驶该轿车从 A 地前往 B 地,到达 B 地时邮箱剩余油量为 22L,求 A,B 两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
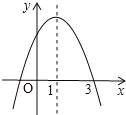
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的有_____.
①abc>0
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3
③2a+b=0
④当x>0时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,AD平分∠BAC,BD=CD

(1)求证:BE=CF;
(2)已知AC=10,DE=4,BE=2,求△AEC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长春市地铁1号线,北起北环站,南至红咀子站,共设15个地下车站,2017年6月30日开通运营,标志着吉林省正式迈进“地铁时代”,15个站点如图所示.

某天,王红从人民广场站开始乘坐地铁,在地铁各站点做志愿者服务,到A站下车时,本次志愿者服务活动结束,约定向红咀子站方向为正,当天的乘车记录如下(单位:站):+5,﹣2,﹣6,+8,+3,﹣4,﹣9,+8
(1)请通过计算说明A站是哪一站?
(2)相邻两站之间的距离为1.3千米,求这次王红志愿服务期间乘坐地铁行进的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图甲是一个长为2a,宽为2b的长方形,沿图甲中虚线用剪刀均匀分成四个小长方形,然后按图乙的形状拼成一个正方形.
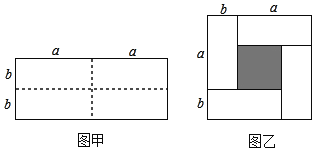
(1)请将图乙中阴影部分正方形的边长用含a、b的代数式表示;
(2)请用两种不同的方法求图乙中阴影部分的面积S;
(3)观察图乙,并结合(2)中的结论,写出下列三个整式:![]() ,
,![]() ,ab之间的等式;
,ab之间的等式;
(4)根据(3)中的等量关系,解决如下问题:当![]() ,
,![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
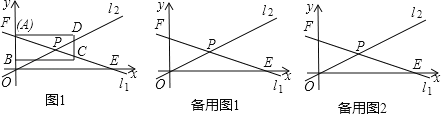
【题目】如图,在平面直角坐标系中,点F的坐标为(0,10).点E的坐标为(20,0),直线l1经过点F和点E,直线l1与直线l2 、y=![]() x相交于点P.
x相交于点P.
(1)求直线l1的表达式和点P的坐标;
(2)矩形ABCD的边AB在y轴的正半轴上,点A与点F重合,点B在线段OF上,边AD平行于x 轴,且AB=6,AD=9,将矩形ABCD沿射线FE的方向平移,边AD始终与x 轴平行.已知矩形ABCD以每秒![]() 个单位的速度匀速移动(点A移动到点E时止移动),设移动时间为t秒(t>0).
个单位的速度匀速移动(点A移动到点E时止移动),设移动时间为t秒(t>0).
①矩形ABCD在移动过程中,B、C、D三点中有且只有一个顶点落在直线l1或l2上,请直接写出此时t的值;
②若矩形ABCD在移动的过程中,直线CD交直线l1于点N,交直线l2于点M.当△PMN的面积等于18时,请直接写出此时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com