
【题目】如图,DE⊥AB于E,DF⊥AC于F,AD平分∠BAC,BD=CD

(1)求证:BE=CF;
(2)已知AC=10,DE=4,BE=2,求△AEC的面积
【答案】(1)证明见解析;(2)36.
【解析】
(1)根据角平分线性质和全等三角形的性质得出即可;
(2)根据全等三角形的判定得出Rt△AED≌Rt△AFD,根据全等三角形的性质得出AE=AF,利用三角形面积公式即可得出答案.
(1)证明:∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,∠DEB=∠DFC=90°,
在Rt△BED和Rt△CFD中
![]() ,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFA=90°,
在Rt△AED和Rt△AFD中
![]() ,
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵Rt△BED≌Rt△CFD,
∴CF=BE,
∵AC=10,BE=2,
∴AE=AF=10-2=8,DE=DF=4,
∴△AEC的面积=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题中:①有限小数是有理数;②无限小数都是无理数;③任意两个无理数的和还是无理数;④开方开不尽的数是无理数;⑤一个数的算术平方根一定是正数;⑥一个数的立方根一定比这个数小;⑦任意两个有理数之间都有有理数,任意两个无理数之间都有无理数.⑧有理数和数轴上的点一一对应;⑨不带根号的数一定是有理数;⑩负数没有立方根.其中正确的有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
(1)求EF的长;
(2)求梯形ABCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为_____厘米/秒,△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解了解节能减排、垃圾分类等知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查调查,调查结果分为“非常了解“、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制出以下两幅不完整的统计图,请根据统计图回答下列问题:
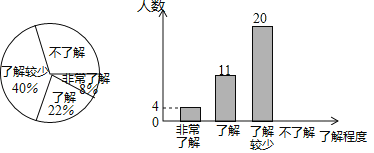
(1)本次调查的学生共有 人,估计该校2000名学生中“不了解”的人数约有 人.
(2)“非常了解”的4人中有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图和列表的方法,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在三角形ABC中,D是BC上一点,且∠CDA=∠CAB.(注:三角形内角和等于180°)

(1)求证:∠CDA=∠DAB+∠DBA;
(2)如图2,MN是经过点D的一条直线,若直线MN交AC边于点E,且∠CDE=∠CAD.求证:∠AED+∠EAB=180°;
(3)将图2中的直线MN绕点D旋转,使它与射线AB交于点P(点P不与点A,B重合).在图3中画出直线MN,并用等式表示∠CAD,∠BDP,∠BPD这三个角之间的数量关系,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
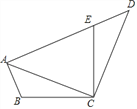
【题目】如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若∠ACB=30°,∠D=45°,求∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)x2+8x-20=0(用配方法);
(2)x2-2x-3=0;
(3)(x-1)(x+2)=4(x-1);
(4)3x2-6x=1(用公式法).
查看答案和解析>>
科目:初中数学 来源: 题型:
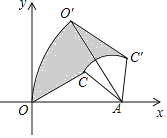
【题目】如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转到△O′AC′,使得点O′的坐标是(1,![]() ),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com