
【题目】如图,在菱形ABCD中,AC与BD相交于点O,AB=4,BD=4![]() ,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )
,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )

A. 4B. 2![]() C. 2
C. 2![]() D. 8
D. 8
科目:初中数学 来源: 题型:
【题目】“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战
士们离营地的距离![]() 与时间
与时间![]() 之间函数关系的是( )
之间函数关系的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P(﹣3,m)和 Q(1,m)是抛物线y=x2+bx﹣3上的两点.

(1)求b的值;
(2)将抛物线y=x2+bx﹣3的图象向上平移k(是正整数)个单位,使平移后的图象与x轴无交点,求k的最小值;
(3)将抛物线y=x2+bx﹣3的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合新图象回答:当直线y=x+n与这个新图象有两个公共点时,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需![]() 天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需
天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需![]() 天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);

(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需要经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°。因城市规划的需要,将在A,B两地之间修建一条笔直的公路。
(1)求改直后的公路AB的长;
(2)问:公路改造后比原来缩短了多少千米?
(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.
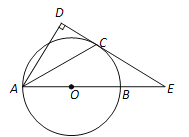
(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过原点,与
经过原点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,将抛物线
,将抛物线![]() 向右平移
向右平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,
, ![]() 交
交![]() 轴于
轴于![]() ,
, ![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),交
的左边),交![]() 轴于点
轴于点![]() .
.


(![]() )求抛物线
)求抛物线![]() 的解析式及顶点坐标.
的解析式及顶点坐标.
(![]() )以
)以![]() 为斜边向上作等腰直角三角形
为斜边向上作等腰直角三角形![]() ,当点
,当点![]() 落在抛物线
落在抛物线![]() 的对称轴上时,求抛物线
的对称轴上时,求抛物线![]() 的解析式.
的解析式.
(![]() )若抛物线
)若抛物线![]() 的对称轴存在点
的对称轴存在点![]() ,使
,使![]() 为等边三角形,请直接写出
为等边三角形,请直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com