
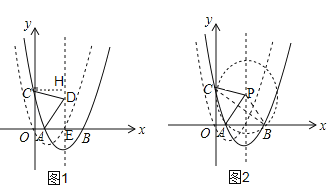
【题目】如图,抛物线![]() 经过原点,与
经过原点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,将抛物线
,将抛物线![]() 向右平移
向右平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,
, ![]() 交
交![]() 轴于
轴于![]() ,
, ![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),交
的左边),交![]() 轴于点
轴于点![]() .
.


(![]() )求抛物线
)求抛物线![]() 的解析式及顶点坐标.
的解析式及顶点坐标.
(![]() )以
)以![]() 为斜边向上作等腰直角三角形
为斜边向上作等腰直角三角形![]() ,当点
,当点![]() 落在抛物线
落在抛物线![]() 的对称轴上时,求抛物线
的对称轴上时,求抛物线![]() 的解析式.
的解析式.
(![]() )若抛物线
)若抛物线![]() 的对称轴存在点
的对称轴存在点![]() ,使
,使![]() 为等边三角形,请直接写出
为等边三角形,请直接写出![]() 的值.
的值.
【答案】(1)抛物线![]() 的解析式为
的解析式为![]() ,顶点坐标
,顶点坐标![]() ;
;
(2)抛物线![]() 的解析式为:
的解析式为: ![]() ;
;
(3)![]() .
.
【解析】试题分析:(1)把(0,0)及(2,0)代入y=x2+bx+c,求出抛物线C1的解析式,即可求出抛物线C1的顶点坐标;
(2)先求出C2的解析式,确定A,B,C的坐标,过点C作CH⊥对称轴DE,垂足为H,利用△PAC为等腰直角三角形,求出角的关系可证得△CHD≌△DEA,再由OC=EH列出方程求解得出m的值,即可得出C2的解析式.
(3)连接BC,BP,由抛物线对称性可知AP=BP,由△PAC为等边三角形,可得AP=BP=CP,∠APC=60°,由C,A,B三点在以点P为圆心,PA为半径的圆上,可得BC=2OC,利用勾股定理求出OB=![]() OC,列出方程求出m的值即可.
OC,列出方程求出m的值即可.
试题解析:解:(1)∵抛物线C1经过原点,与x轴的另一个交点为(2,0),∴![]() ,解得:
,解得: ![]() ,∴抛物线C1的解析式为y=x2﹣2x,∴抛物线C1的顶点坐标(1,﹣1);
,∴抛物线C1的解析式为y=x2﹣2x,∴抛物线C1的顶点坐标(1,﹣1);
(2)如图1,∵抛物线C1向右平移m(m>0)个单位得到抛物线C2,∴C2的解析式为y=(x﹣m﹣1)2﹣1,∴A(m,0),B(m+2,0),C(0,m2+2m),过点C作CH⊥对称轴DE,垂足为H,∵△ACD为等腰直角三角形,∴AD=CD,∠ADC=90°,∴∠CDH+∠ADE=90°,∴∠HCD=∠ADE,∵∠DEA=90°,∴△CHD≌△DEA,∴AE=HD=1,CH=DE=m+1,∴EH=HD+DE=1+m+1=m+2,由OC=EH得m2+2m=m+2,解得m1=1,m2=﹣2(舍去),∴抛物线C2的解析式为:y=(x﹣2)2﹣1.
(3)如图2,连接BC,BP,由抛物线对称性可知AP=BP,∵△PAC为等边三角形,∴AP=BP=CP,∠APC=60°,∴C,A,B三点在以点P为圆心,PA为半径的圆上,∴∠CBO=![]() ∠CPA=30°,∴BC=2OC,∴由勾股定理得OB=
∠CPA=30°,∴BC=2OC,∴由勾股定理得OB=![]() =
=![]() OC,∴
OC,∴![]() (m2+2m)=m+2,解得m1=
(m2+2m)=m+2,解得m1=![]() ,m2=﹣2(舍去),∴m=
,m2=﹣2(舍去),∴m=![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )

A. 8 B. 16 C. 24 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1)、P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且﹣1<x1<x2,x3<﹣1,则y1、y2、y3的大小关系为( )

A. y1<y2<y3 B. y3<y1<y2 C. y3<y2<y1 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的体能情况,随机抽取部分男生进行引体向上测试,并根据抽测成绩绘制成如下两幅统计图.


(![]() )本次抽测的学生总人数为__________;请你补全图
)本次抽测的学生总人数为__________;请你补全图![]() 的统计图.
的统计图.
(![]() )本次抽测成绩的众数为__________次;中位数为__________次.
)本次抽测成绩的众数为__________次;中位数为__________次.
(![]() )若规定引体向上
)若规定引体向上![]() 次以上(含
次以上(含![]() 次)为体能达到优秀,则该校
次)为体能达到优秀,则该校![]() 名九年级男生中,估计有多少人能达到优秀?
名九年级男生中,估计有多少人能达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=42°,∠DAE=30°,则α= ,β= .
②若∠BAC=54°,∠DAE=36°,则α= ,β= .
③写出α与β的数量关系,并说明理由;

(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
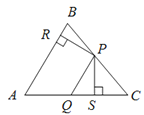
【题目】如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS![]() AC,PR
AC,PR![]() AB,若AQ
AB,若AQ![]() PQ,PR
PQ,PR![]() PS,则下列结论:①AS
PS,则下列结论:①AS![]() AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ=
AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ=![]() .其中正确的结论有____________(填序号).
.其中正确的结论有____________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中,△ABC不是直角三角形的是 ( )
A. b2=a2-c2 B. ∠A:∠B:∠C=3:4:5
C. ∠C=∠A-∠B D. a2:b2:c2=1:3:2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com