【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=﹣1，P1（x1，y1）、P2（x2，y2）是抛物线上的点，P3（x3，y3）是直线l上的点，且﹣1＜x1＜x2，x3＜﹣1，则y1、y2、y3的大小关系为（ ）
A. y1＜y2＜y3 B. y3＜y1＜y2 C. y3＜y2＜y1 D. y2＜y1＜y3
科目：初中数学 来源： 题型：
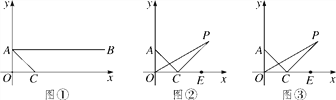
【题目】如图①，在平面直角坐标系中，A(0，1)，B(4，1)，C为x轴正半轴上一点，且AC平分∠OAB.
(1)求证：∠OAC＝∠OCA；
(2)如图②，若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于点P，即满足∠POC＝
∠AOC，∠PCE＝
∠ACE，求∠P的大小；
(3)如图③，在(2)中，若射线OP、CP满足∠POC＝
∠AOC，∠PCE＝
∠ACE，猜想∠OPC的大小，并证明你的结论(用含n的式子表示)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在正方形ABCD中，AB＝6，P为边CD上一点，过P点作PE⊥BD于点E，连接BP.
(1) 如图1，求 
的值；
(2)O为BP的中点，连接CO并延长交BD于点F.
① 如图2，连接OE，求证：OE⊥OC；
② 如图3，若
，求DP的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，要在木里县某林场东西方向的两地之间修一条公路MN，已知点C周围200 m范围内为原始森林保护区，在MN上的点A处测得C在A的北偏东45°方向上，从A向东走600 m到达B处，测得C在点B的北偏西60°方向上.
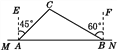
（1）MN是否穿过原始森林保护区?为什么?(参考数据: 
≈1.732)
（2）若修路工程顺利进行，要使修路工程比原计划提前5天完成，需将原定的工作效率提高25%，则原计划完成这项工程需要多少天?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y1=kx+b的图象与反比例函数
的图象交于A（﹣2，1），B（1，n）两点．
（1）试确定上述反比例函数和一次函数的表达式．
（2）求△AOB的面积．
（3）比较y1和y2的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
经过原点，与
轴的另一个交点为
，将抛物线
向右平移
个单位得到抛物线
， 
交
轴于
， 
两点（点
在点
的左边），交
轴于点
．
（
）求抛物线
的解析式及顶点坐标．
（
）以
为斜边向上作等腰直角三角形
，当点
落在抛物线
的对称轴上时，求抛物线
的解析式．
（
）若抛物线
的对称轴存在点
，使
为等边三角形，请直接写出
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图：在正方形网格中有一个△ABC，按要求进行下列作图（只能借助于网格）：
（1）画出△ABC中BC边上的高AD；
（2）画出先将△ABC向右平移6格，再向上平移3格后的△A1B1C1；
（3）画一个△BCP（要求各顶点在格点上，P不与A点重合），使其面积等于△ABC的面积．并回答，满足这样条件的点P共________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
