
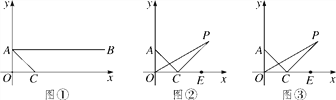
����Ŀ����ͼ������ƽ��ֱ������ϵ�У�A(0��1)��B(4��1)��CΪx����������һ�㣬��ACƽ����OAB.
(1)��֤����OAC����OCA��
(2)��ͼ�������ֱ�����AOC�����ȷ�����OCA����ǵ����ȷ��߽��ڵ�P���������POC��![]() ��AOC����PCE��
��AOC����PCE��![]() ��ACE�����P�Ĵ�С��
��ACE�����P�Ĵ�С��
(3)��ͼ�ۣ���(2)�У�������OP��CP�����POC��![]() ��AOC����PCE��
��AOC����PCE��![]() ��ACE�������OPC�Ĵ�С����֤����Ľ���(�ú�n��ʽ�ӱ�ʾ)��
��ACE�������OPC�Ĵ�С����֤����Ľ���(�ú�n��ʽ�ӱ�ʾ)��
���𰸡���1��֤����������2��15�㣨3��![]()
�������������������1������AB���������á�OAB��С�����ݽ�ƽ�������ʿ���á�OAC��С�����ɽ��⣻
��2����������и����ġ�POC=![]() ��AOC����PCE=
��AOC����PCE=![]() ��ACE������á�PCE�͡�POC�Ĵ�С���ٸ�����������ǵ��ڲ��������ڽǺͼ��ɽ��⣻
��ACE������á�PCE�͡�POC�Ĵ�С���ٸ�����������ǵ��ڲ��������ڽǺͼ��ɽ��⣻
��3���ⷨ�ͣ�2����ͬ����������и����ġ�POC=![]() ��AOC����PCE=
��AOC����PCE=![]() ��ACE������á�PCE�͡�POC�Ĵ�С���ٸ�����������ǵ��ڲ��������ڽǺͼ��ɽ��⣮
��ACE������á�PCE�͡�POC�Ĵ�С���ٸ�����������ǵ��ڲ��������ڽǺͼ��ɽ��⣮
���������(1)֤������A(0��1)��B(4��1)����AB��CO�����OAB��180������AOC��90��.
��ACƽ�֡�OAB�����OAC��45�������OCA��90����45����45�������OAC����OCA.
(2)�⣺�ߡ�POC��![]() ��AOC�����POC��
��AOC�����POC��![]() ��90����30��.�ߡ�PCE��
��90����30��.�ߡ�PCE��![]() ��ACE�����PCE��
��ACE�����PCE��![]() (180����45��)��45��.�ߡ�P����POC����PCE�����P����PCE����POC��15��.
(180����45��)��45��.�ߡ�P����POC����PCE�����P����PCE����POC��15��.
(3)�⣺��OPC��![]() .
.
֤�����£��ߡ�POC��![]() ��AOC�����POC��
��AOC�����POC��![]() ��90����
��90����![]() .�ߡ�PCE��
.�ߡ�PCE��![]() ��ACE�����PCE��
��ACE�����PCE��![]() (180����45��)��
(180����45��)��![]() .
.
�ߡ�OPC����POC����PCE��
���OPC����PCE����POC��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е��飺
���˽�ij�����ӵķ�ѿ�� ���˽�ij��ѧ���ԡ����������ļ�ֵ�ۡ���֪����
���˽�ij��������ˮˮ�� ���˽����꼶��1����ѧ���μӡ������Կ�ѧʵ�������ɴ���
�ʺϲ�ȡȫ�������ǣ� ��
A.�٢�B.�ڢ�C.�٢�D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
�� ![]() ����
����![]() ��
��![]() �ֱ�������
�ֱ�������![]() ������
������![]() �ϣ�����
�ϣ�����![]() ���
���![]() ����
����![]() �Գƣ���
�Գƣ���![]() ��
��![]() ����
����![]() �Գƣ�
�Գƣ� ![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() �����������⣺��
�����������⣺��![]() ����
����![]() ������
������![]() ��
�� ![]() ����
����![]() �ǵ���ֱ�������Σ�����ȷ�������У� ����
�ǵ���ֱ�������Σ�����ȷ�������У� ����

A. ![]() �� B.
�� B. ![]() �� C.
�� C. ![]() �� D.
�� D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ε�ÿ���ڽǶ��������ڵ���ǵ�4����30�㣬���������ε��ڽǺͼ��Խ��ߵ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
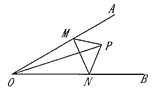
����Ŀ����ͼ��ʾ����AOB���ڲ���һ��P��������O�ľ���Ϊ5cm��M��N�ֱ�������OA��OB�ϵĶ��㣮����AOB =30![]() �����PMN�ܳ�����СֵΪ________.
�����PMN�ܳ�����СֵΪ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ���������ݣ��ٽ������.
���⣺��![]() , ��m��n��ֵ
, ��m��n��ֵ
�⣺��![]()
��![]()
��![]()
��![]() ��
�� ![]()
��![]() ��
�� ![]()
���⣺(1)��![]() ����
����![]() ��ֵ��
��ֵ��
(2)��֪a��b��c�ǡ�ABC�����߳�������![]() ,��c�ǡ�ABC����ıߣ���c��ȡֵ��Χ��
,��c�ǡ�ABC����ıߣ���c��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��MON=30������A1��A2��A3����������ON�ϣ���B1��B2��B3����������OM�ϣ���A1B1A2����A2B2A3����A3B3A4������Ϊ�ȱ������Σ���OA1=2������A5B5A6�ı߳�Ϊ( )

A. 8 B. 16 C. 24 D. 32
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ߺ�ֱ��l��ͬһֱ������ϵ�е�ͼ����ͼ��ʾ�������ߵĶԳ���Ϊֱ��x=��1��P1��x1��y1����P2��x2��y2�����������ϵĵ㣬P3��x3��y3����ֱ��l�ϵĵ㣬�ҩ�1��x1��x2��x3����1����y1��y2��y3�Ĵ�С��ϵΪ��������

A. y1��y2��y3 B. y3��y1��y2 C. y3��y2��y1 D. y2��y1��y3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com