
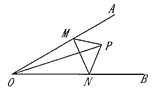
【题目】如图所示:∠AOB的内部有一点P,到顶点O的距离为5cm,M、N分别是射线OA、OB上的动点.若∠AOB =30![]() ,则△PMN周长的最小值为________.
,则△PMN周长的最小值为________.
【答案】5cm
【解析】分别作点P关于OA、OB的对称点C.D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.
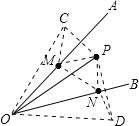
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=5cm,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60,
∴△COD是等边三角形,
∴CD=OC=OD=5cm.
∴△PMN的周长的最小值=PM+MN+PN=CM+MN+DNCD=5cm.
∴△PMN周长的最小值为5cm.
点睛: 本题考查了轴对称-最短路线问题, 设点P关于OA的对称点为C,关于OB的对称点为D,当点M、N在CD上时,△PMN的周长最小.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】已知在四边形![]() 中,∠A=∠C=90°.
中,∠A=∠C=90°.
(1)如图1,若BE平分∠ABC,DF平分∠ADC的邻补角,请写出BE与DF的位置关系,并证明.

(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.

(3)如图3,若BE、DE分别五等分∠ABC、∠ADC的邻补角(即∠CDE=![]() ,∠CBE=
,∠CBE=![]() ),则∠E= .
),则∠E= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由边长为1个单位长度的小正方形组成的网格图.
(1)请在图中建立平面直角坐标系,使A、B两点的坐标分别为A(2,3)、B(-2,0);
(2)正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形,在图中画出格点△ABC使得AB=AC,请写出在(1)中所建坐标系内所有满足条件的点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=7°,一条光线从点A出发后射向OB边.若光线与OB边垂直,则光线沿原路返回到点A,此时∠A=90°-7°=83°.当∠A<83°时,光线射到OB边上的点A1后,经OB反射到线段AO上的点A2,易知∠1=∠2.若A1A2⊥AO,光线又会沿A2→A1→A原路返回到点A,此时∠A=76°.…若光线从A点出发后,经若干次反射能沿原路返回到点A,则锐角∠A的最小值为______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
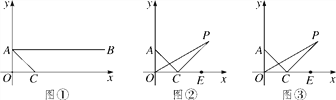
【题目】如图①,在平面直角坐标系中,A(0,1),B(4,1),C为x轴正半轴上一点,且AC平分∠OAB.
(1)求证:∠OAC=∠OCA;
(2)如图②,若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于点P,即满足∠POC=![]() ∠AOC,∠PCE=
∠AOC,∠PCE=![]() ∠ACE,求∠P的大小;
∠ACE,求∠P的大小;
(3)如图③,在(2)中,若射线OP、CP满足∠POC=![]() ∠AOC,∠PCE=
∠AOC,∠PCE=![]() ∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示).
∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四块长为a,宽为b的长方形木板围成如图所示的正方形,请解答下列问题:
(1)按要求用含a,b的式子表示空心部分的正方形的面积S(结果不要化简,保留原式):
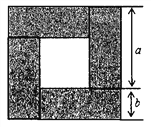
①用大正方形面积减去四块木板的面积表示:S= ;
②直接用空心部分的正方形边长的平方表示:S= ;
(2)由①、②可得等式 ;
(3)用整式的乘法验证(2)中的等式成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我省启动了“关爱留守儿童工程”.某村小为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )
A.平均数是15 B.众数是10 C.中位数是17 D.方差是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com