
【题目】如图,一次函数y1=kx+b的图象与反比例函数![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式.
(2)求△AOB的面积.
(3)比较y1和y2的大小.

【答案】(1)![]() ,y=﹣x﹣1;(2)1.5;(3)当x<﹣2或0<x<1时,y1>y2;当﹣2<x<0或x>1时,y1<y2.
,y=﹣x﹣1;(2)1.5;(3)当x<﹣2或0<x<1时,y1>y2;当﹣2<x<0或x>1时,y1<y2.
【解析】试题分析: (1)把A的坐标代入反比例函数的解析式,即可求出反比例函数的解析式,把B的坐标代入求出B的坐标,把A、B的坐标代入一次函数y1=kx+b即可求出函数的解析式;
(2)求出C的坐标,求出△AOC和△BOC的面积,即可求出答案;
(3)根据函数的图象和A、B的坐标即可得出答案.
试题解析:
解:(1)∵把A(﹣2,1)代入y2=![]() 得:m=﹣2,
得:m=﹣2,
∴反比例函数的解析式是y=﹣![]() ,
,
∵B(1,n)代入反比例函数y=﹣![]() 得:n=﹣2,
得:n=﹣2,
∴B的坐标是(1,﹣2),
把A、B的坐标代入一次函数y1=kx+b得:
![]() ,
,
解得:k=﹣1,b=﹣1,
∴一次函数的解析式是y=﹣x﹣1;
(2)∵把y=0代入一次函数的解析式是y=﹣x﹣1得:
0=﹣x﹣1,
解得x=﹣1,
∴C(﹣1,0),
∴S△AOB=SAOC+S△BOC=![]() ×|﹣1|×1+
×|﹣1|×1+![]() ×|﹣1|×|﹣2|=1.5;
×|﹣1|×|﹣2|=1.5;
(3)从图象可知:
当x<﹣2或0<x<1时,y1>y2;
当﹣2<x<0或x>1时,y1<y2.

点睛: 本题考查一次函数和反比例函数的交点问题,用待定系数法求一次函数的解析式,三角形的面积等知识点的综合运用,主要考查学生的计算能力和观察图形的能力,以及数形结合思想的运用.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题.
例题:若![]() , 求m和n的值
, 求m和n的值
解:∵![]()
∴![]()
∴![]()
∴![]() ,
, ![]()
∴![]() ,
, ![]()
问题:(1)若![]() ,求
,求![]() 的值.
的值.
(2)已知a,b,c是△ABC的三边长,满足![]() ,且c是△ABC中最长的边,求c的取值范围.
,且c是△ABC中最长的边,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程 ![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围。
(2)是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1)、P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且﹣1<x1<x2,x3<﹣1,则y1、y2、y3的大小关系为( )

A. y1<y2<y3 B. y3<y1<y2 C. y3<y2<y1 D. y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的体能情况,随机抽取部分男生进行引体向上测试,并根据抽测成绩绘制成如下两幅统计图.


(![]() )本次抽测的学生总人数为__________;请你补全图
)本次抽测的学生总人数为__________;请你补全图![]() 的统计图.
的统计图.
(![]() )本次抽测成绩的众数为__________次;中位数为__________次.
)本次抽测成绩的众数为__________次;中位数为__________次.
(![]() )若规定引体向上
)若规定引体向上![]() 次以上(含
次以上(含![]() 次)为体能达到优秀,则该校
次)为体能达到优秀,则该校![]() 名九年级男生中,估计有多少人能达到优秀?
名九年级男生中,估计有多少人能达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
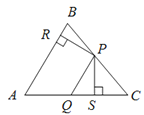
【题目】如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS![]() AC,PR
AC,PR![]() AB,若AQ
AB,若AQ![]() PQ,PR
PQ,PR![]() PS,则下列结论:①AS
PS,则下列结论:①AS![]() AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ=
AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ=![]() .其中正确的结论有____________(填序号).
.其中正确的结论有____________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与x轴交于点A,与y轴交于点B.点C是x轴上一动点,点D为(3,0),抛物线
与x轴交于点A,与y轴交于点B.点C是x轴上一动点,点D为(3,0),抛物线![]() 过B、C、D三点.
过B、C、D三点.
(1)如图1所示,若点C与点A关于y轴对称.
①求直线BD和抛物线的解析式;
②若点P是抛物线对称轴上一动点,当BP+CP的值最小时,求点P的坐标;
③若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标;
(2)如图2,若BE//x轴,且E(4,3),点A1与点A关于直线BC对称,当EA1的长最小时,直接写出OC的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com