
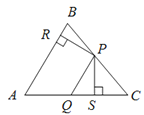
【题目】如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS![]() AC,PR
AC,PR![]() AB,若AQ
AB,若AQ![]() PQ,PR
PQ,PR![]() PS,则下列结论:①AS
PS,则下列结论:①AS![]() AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ=
AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ=![]() .其中正确的结论有____________(填序号).
.其中正确的结论有____________(填序号).
科目:初中数学 来源: 题型:
【题目】已知:在正方形ABCD中,AB=6,P为边CD上一点,过P点作PE⊥BD于点E,连接BP.

(1) 如图1,求 ![]() 的值;
的值;
(2)O为BP的中点,连接CO并延长交BD于点F.
① 如图2,连接OE,求证:OE⊥OC;
② 如图3,若![]() ,求DP的长.
,求DP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式.
(2)求△AOB的面积.
(3)比较y1和y2的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过原点,与
经过原点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,将抛物线
,将抛物线![]() 向右平移
向右平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,
, ![]() 交
交![]() 轴于
轴于![]() ,
, ![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),交
的左边),交![]() 轴于点
轴于点![]() .
.


(![]() )求抛物线
)求抛物线![]() 的解析式及顶点坐标.
的解析式及顶点坐标.
(![]() )以
)以![]() 为斜边向上作等腰直角三角形
为斜边向上作等腰直角三角形![]() ,当点
,当点![]() 落在抛物线
落在抛物线![]() 的对称轴上时,求抛物线
的对称轴上时,求抛物线![]() 的解析式.
的解析式.
(![]() )若抛物线
)若抛物线![]() 的对称轴存在点
的对称轴存在点![]() ,使
,使![]() 为等边三角形,请直接写出
为等边三角形,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏果超市用5000元购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨11000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍。
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种的苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?(7分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为________________________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com