
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.
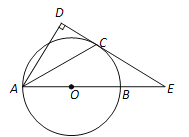
(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)连接OC,根据条件先证明OC∥AD,然后证出OC⊥CD即可;(2)先利用勾股定理求出AE的长,再根据条件证明△ECO∽△EDA,然后利用对应边成比例求出OC的长,再根据BE=AE﹣2OC计算即可.
试题解析:(1)证明:连接OC,

∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵OC=OA,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∵OC为⊙O半径,
∴CD是⊙O的切线.
(2)解:在Rt△ADE中,由勾股定理得:AE=![]() =15,
=15,
∵OC∥AD,
∴△ECO∽△EDA,
∴![]()
∴![]()
解得:OC=![]() ,
,
∴BE=AE﹣2OC=15﹣2×![]() =
=![]() ,
,
答:BE的长是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=-![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线![]() =ax2+bx+
=ax2+bx+![]() 经过A、B两点.
经过A、B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M从作MH⊥BC于点H,作轴MD∥y轴交BC于点D,求![]() DMH周长的最大值.
DMH周长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD的边长为3,∠BAD=60°.
(1)连接AC,过点D作DE⊥AB于点E,DF⊥BC交AC于点F,DE、DF于点M、N.
①依题意补全图1;
②求MN的长;
(2)如图2,将(1)中∠EDF以点D为中心,顺时针旋转45°,其两边DE′、DF′分别与直线AB、BC相交于点Q、P,连接QP,请写出求△DPQ的面积的思路.(可以不写出计算结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC与BD相交于点O,AB=4,BD=4![]() ,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )
,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )

A. 4B. 2![]() C. 2
C. 2![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大润发超市在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,超市应将这种商品的售价定为多少?
(2)设每件商品的售价为x元,超市所获利润为y元.
①求y与x之间的函数关系式;
②物价局规定该商品的售价不能超过40元/件,超市为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图在ABCD中,点E为AB上一点,连接CE、DE,且CE⊥AB,CE=AB,点F为BC上一点,连接DF交CE于点G,∠CGD=∠B;

(1)若CG=2,AD=3,求GE的长;
(2)若CF=![]() DE,求证:AD=CG+BE.
DE,求证:AD=CG+BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
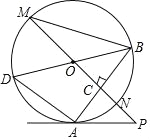
【题目】如图,已知⊙O中,AB为弦,直线PO交⊙O于点M、N,PO⊥AB于C,过点B作直径BD,连接AD、BM、AP.
(1)求证:PM∥AD;
(2)若∠BAP=2∠M,求证:PA是⊙O的切线;
(3)若AD=6,tan∠M=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买![]() 、
、![]() 两种型号的机器人搬运材料,已知
两种型号的机器人搬运材料,已知![]() 型机器人比
型机器人比![]() 型机器人每小时多搬运
型机器人每小时多搬运![]() 材料,且
材料,且![]() 型机器人搬运
型机器人搬运![]() 的材料所用的时间与
的材料所用的时间与![]() 型机器人搬运
型机器人搬运![]() 材料所用的时间相同.
材料所用的时间相同.
(1)求![]() 、
、![]() 两种型号的机器人每小时分别搬运多少材料?
两种型号的机器人每小时分别搬运多少材料?
(2)该公司计划采购![]() 、
、![]() 两种型号的机器人共
两种型号的机器人共![]() 台,要求每小时搬运的材料不得少于
台,要求每小时搬运的材料不得少于![]() ,则至少购进
,则至少购进![]() 型机器人多少台?
型机器人多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com