
【题目】如图,直线y=-![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线![]() =ax2+bx+
=ax2+bx+![]() 经过A、B两点.
经过A、B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M从作MH⊥BC于点H,作轴MD∥y轴交BC于点D,求![]() DMH周长的最大值.
DMH周长的最大值.

【答案】(1) 点A的坐标为(-1,0); (2) y=-![]() x2+
x2+![]() x+
x+![]() (3)
(3)![]() .
.
【解析】
试题(1)、根据直线的函数解析式求出点B和点C的坐标,然后根据△AOC和△COB相似得出点A的坐标;(2)、将点A和点B的坐标代入函数解析式,利用待定系数法求出函数解析式;(3)、由题意知,△DMH为直角三角形,且∠M=30°,当MD取得最大值时,△DMH的周长最大;设出点M的坐标,从而得出点D的坐标,然后利用做差法得出MD的长度,利用函数的性质求出MD的最大值,从而根据特殊直角三角形的性质得出周长的最大值.
试题解析:解: (1)∵直线y=-![]() x+
x+![]() ;分别与x轴、y轴交于B、C两点,
;分别与x轴、y轴交于B、C两点,
∴点B的坐标为(3,0),点C的坐标为(0,![]() );
);
∴∠ACO+∠BCO=90°,∠ACO+∠CAO=90°, ∴∠CAO=∠BCO,
∵∠AOC=∠COB=90°, ∴△AOC∽△COB, ∴![]() .∴
.∴![]() =
=![]() ,∴AO=1,
,∴AO=1,
∴点A的坐标为(-1,0).
(2)∵抛物线y=ax2+bx+![]() ;经过A、B两点,
;经过A、B两点,
∴![]() ,解得:
,解得: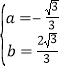 , ∴抛物线的解析式为y=-
, ∴抛物线的解析式为y=-![]() x2+
x2+![]() x+
x+![]() ;
;
(3)由题意知,△DMH为直角三角形,且∠M=30°,当MD取得最大值时,△DMH的周长最大.
设M(x,-![]() x2+
x2+![]() x+
x+![]() ), D(x,-
), D(x,-![]() x+
x+![]() ), 则MD=(-
), 则MD=(-![]() x2+
x2+![]() x+
x+![]() )-(-
)-(-![]() x+
x+![]() ),
),
即:MD=-![]() x2+
x2+![]() x(0<x<3), MD=-
x(0<x<3), MD=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∴当x=![]() 时,MD有最大值
时,MD有最大值![]() ,
,
∴△DMH周长的最大值为![]() +
+![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某企业有5名正副经理,100名工人,年底公布经营业绩,如下表所示:
2002年 | 2003年 | 2004年 | |
5名正副经理红利总额 | 5万元 | 7.5万元 | 10万元 |
100名工人工资总额 | 10万元 | 12.5万元 | 15万元 |
你认为最恰当的是( )

A. 经理所画的图a
B. 工会主席所画的图b
C. 工人所画的图c
D. 都正确,只不过考虑的角度不同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD,延长AD到E,使DE=AD,连接BE与DC交于O点.

(1)求证:△BOC≌△EOD;
(2)当△ABE满足什么条件时,四边形BCED是菱形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战
士们离营地的距离![]() 与时间
与时间![]() 之间函数关系的是( )
之间函数关系的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在证明“有两个角相等的三角形是等腰三角形”这一命题时, 画出图形,写出“己知”、“求证”(如图),他对 辅助线描述如下:“过点A作BC的中垂线AD,垂足为D”.

(1)请你简要说明小明的辅助线作法错在哪里?
(2)请你正确完整地写出这一命题的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点C1在边BC上,将△C1CD绕点D顺时针旋转90°得到△A1AD.A1F平分∠BA1C1,交BD于点F,过点F作FE⊥A1C1,垂足为E,当A1E=3,C1E=2时,则BD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.
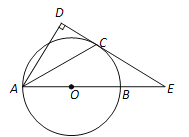
(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com