
【题目】小明在证明“有两个角相等的三角形是等腰三角形”这一命题时, 画出图形,写出“己知”、“求证”(如图),他对 辅助线描述如下:“过点A作BC的中垂线AD,垂足为D”.

(1)请你简要说明小明的辅助线作法错在哪里?
(2)请你正确完整地写出这一命题的证明过程.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如果正方形网格中的每一个小正方形边长都是1,则每个小格的顶点叫做格点.
(1)在图a中以格点为顶点画一个三角形,使三角形的三边长分别为3、![]() 、2
、2![]() ;
;
(2)在图b中以格点为顶点画一个面积为10的正方形;
(3)观察图c中带阴影的图形,请你将它适当剪开,重新拼成一个正方形;(要求:在图c中用虚线作出,并用文字说明剪拼方法)图c说明: .
(4)观察正方体,沿着一些棱将它剪开,展开成平面图形.若正方体的表面积为12,请你在图d中以格点为顶点画出一个正方体的平面展开图.(只需画出一种情形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生汉字书写的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试方法是:听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩x(分) | 频数(人数) | 频率 |
一 | 50≤x<60 | 2 | 0.04 |
二 | 60≤x<70 | 10 | 0.2 |
三 | 70≤x<80 | 14 | b |
四 | 80≤x<90 | a | 0.32 |
五 | 90≤x<100 | 8 | 0.16 |
请根据表格提供的信息,解答以下问题:

(1)直接写出表中a=________,b=________;
(2)请补全右面相应的频数分布直方图;
(3)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为________.
(4)请根据得到的统计数据,简要分析这些同学的汉字书写能力,并为提高同学们的书写汉字能力提一条建议(所提建议不超过20字).
查看答案和解析>>
科目:初中数学 来源: 题型:
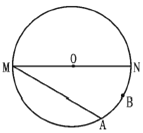
【题目】如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为![]() 的中点,P是直径MN上一动点.
的中点,P是直径MN上一动点.
(1)利用尺规作图,确定当PA+PB最小时P点的位置(不写作法,但要保留作图痕迹).
(2)求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线![]() =ax2+bx+
=ax2+bx+![]() 经过A、B两点.
经过A、B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M从作MH⊥BC于点H,作轴MD∥y轴交BC于点D,求![]() DMH周长的最大值.
DMH周长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=![]() (
(![]() ),将线段BC绕点B逆时针旋转60°得到线段BD。
),将线段BC绕点B逆时针旋转60°得到线段BD。

(1)如图1,直接写出∠ABD的大小(用含![]() 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正整数,由N个数字组成,若它的第一位数可以被1整除,它的前两位数可以被2整除,前三位数可以被3整除,…,一直到前N位数可以被N整除,则这样的数叫做“精巧数”.如:123的第一位数“1”可以被1整除,前两位数“12”可以被2整除,“123”可以被3整除,则123是一个“精巧数”.
(1)若四位数![]() 是一个“精巧数”,求k的值;
是一个“精巧数”,求k的值;
(2)若一个三位“精巧数”![]() 各位数字之和为一个完全平方数,请求出所有满足条件的三位“精巧数”.
各位数字之和为一个完全平方数,请求出所有满足条件的三位“精巧数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.
(1)求抛物线的解析式;
(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值?如果是,请求出此定值;如果不是,请说明理由;
(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图在ABCD中,点E为AB上一点,连接CE、DE,且CE⊥AB,CE=AB,点F为BC上一点,连接DF交CE于点G,∠CGD=∠B;

(1)若CG=2,AD=3,求GE的长;
(2)若CF=![]() DE,求证:AD=CG+BE.
DE,求证:AD=CG+BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com