
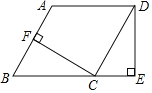
【题目】如图,在ABCD中,CF⊥AB于点F,过点D作DE⊥BC的延长线于点E,且CF=DE.
(1)求证:△BFC≌△CED;
(2)若∠B=60°,AF=5,求BC的长.
【答案】(1)详见解析;(2)BC=10.
【解析】
(1)由平行四边形的性质可得AB∥CD,可得∠B=∠DCE,由“AAS”可证△BFC≌△CED;
(2)设BC=CD=AB=x,由直角三角形的性质可得(x﹣5)=![]() x,可求x的值,即可求BC的长.
x,可求x的值,即可求BC的长.
(1)证明:∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
∴∠B=∠DCE
∵CF⊥AB,DE⊥BC,
∴∠CFB=∠DEC=90°,且CF=DE,∠B=∠DCE
∴△BFC≌△CED (AAS)
(2)∵△BFC≌△CED
∴BC=DC=AB
设BC=x,
∴CD=AB=x
在Rt△BCF中,∠B=60°
∴∠BCF=30°
∴FB=![]() BC
BC
∴(x﹣5)=![]() x
x
解得x=10
∴BC=10.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,如图,作正方形
,如图,作正方形![]() ,点
,点![]() 在直线
在直线![]() 上,点
上,点![]() 在
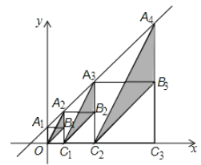
在![]() 轴上,将图中阴影部分三角形的面积从左到右依次记为
轴上,将图中阴影部分三角形的面积从左到右依次记为![]() ,则
,则
(1)![]() 的值为___________;
的值为___________;
(2)![]() 的值为___________.(含
的值为___________.(含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
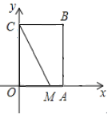
【题目】定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() ,点
,点![]() ,在边
,在边![]() 存在点
存在点![]() ,使得
,使得![]() 为“智慧三角形”,则点
为“智慧三角形”,则点![]() 的坐标为:______.
的坐标为:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_______(只填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,如图2,△ABC以点A为旋转中心顺时针旋转.
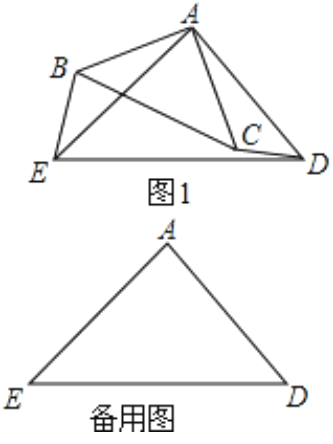
(1)证明:BE=CD
(2)当AC=![]() ED时,探究在△ABC旋转的过程中,是否存在这样的旋转角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,求出角α的度数;若不存在,请说明理由.
ED时,探究在△ABC旋转的过程中,是否存在这样的旋转角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,求出角α的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,甲、乙两家水果店以同样的价格销售同一种水果,它们的优惠方案分别为:甲水果店,一次性购水果超过![]() 元,超过部分打七折;乙水果店,一次性购水果超过
元,超过部分打七折;乙水果店,一次性购水果超过![]() 元,超过部分打五折,设水果售价为
元,超过部分打五折,设水果售价为![]() (单位:元)
(单位:元)![]() ,在甲.乙两家水果店购水果应付金额为
,在甲.乙两家水果店购水果应付金额为![]() (单位:元),
(单位:元),![]() (单位:元),
(单位:元),![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
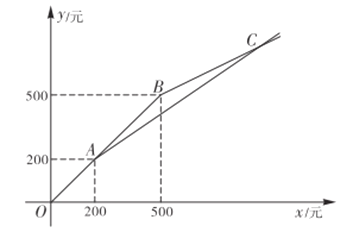
(1)求甲水果店购水果应付金额![]() 与水果售价
与水果售价![]() 之间的函数关系式;
之间的函数关系式;
(2)求交点![]() 的坐标;
的坐标;
(3)根据图象,请直接写出春节期间选择哪家水果店购水果更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
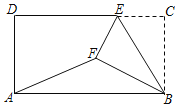
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
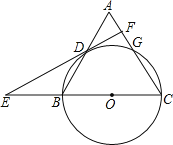
【题目】如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.
(1)求证:DF⊥AC;
(2)求tan∠E的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com