
【题目】如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.
(1)求证:DF⊥AC;
(2)求tan∠E的值.
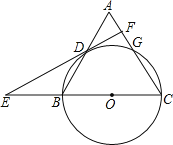
【答案】(1)证明见解析;(2)tan∠CBG=![]() .
.
【解析】(1)连接OC,CD,根据圆周角定理得∠BDC=90°,由等腰三角形三线合一的性质得:D为AB的中点,所以OD是中位线,由三角形中位线性质得:OD∥AC,根据切线的性质可得结论;
(2)如图,连接BG,先证明EF∥BG,则∠CBG=∠E,求∠CBG的正切即可.
(1)证明:如图,连接OC,CD,
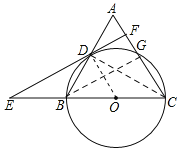
∵BC是⊙O的直径,
∴∠BDC=90°,
∴CD⊥AB,
∵AC=BC,
∴AD=BD,
∵OB=OC,
∴OD是△ABC的中位线
∴OD∥AC,
∵DF为⊙O的切线,
∴OD⊥DF,
∴DF⊥AC;
(2)解:如图,连接BG,
∵BC是⊙O的直径,
∴∠BGC=90°,
∵∠EFC=90°=∠BGC,
∴EF∥BG,
∴∠CBG=∠E,
Rt△BDC中,∵BD=3,BC=5,
∴CD=4,
S△ABC=![]() ,
,
6×4=5BG,
BG=![]() ,
,
由勾股定理得:CG=![]() ,
,
∴tan∠CBG=tan∠E=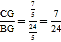 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
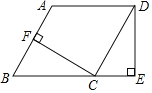
【题目】如图,在ABCD中,CF⊥AB于点F,过点D作DE⊥BC的延长线于点E,且CF=DE.
(1)求证:△BFC≌△CED;
(2)若∠B=60°,AF=5,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
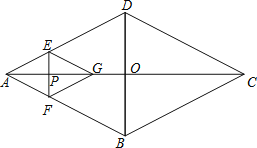
【题目】菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,动点P在线段AC上从点A向点C以4个单位/秒的速度运动,过点P作EF⊥AC,交菱形ABCD的边于点E、F,在直线AC上有一点G,使△AEF与△GEF关于EF对称.设菱形ABCD被四边形AEGF盖住部分的面积为S1,未被盖住部分的面积为S2,点P运动时间为x秒.
(1)用含x的代数式分别表示S1,S2;
(2)若S1=S2,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=8,AD=17,折叠纸片使点B落在边AD上的E处,折痕为PQ.当E在AD边上移动时,折痕的端点P,Q也随着移动.若限定P,Q分别在边BA,BC上移动,则点E在边AD上移动的最大距离为( )
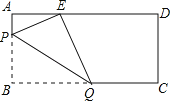
A.6B.7C.8D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,平面直角坐标系中,直线 y1=x+3与抛物线y2=﹣![]() +2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()
+2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,过二次函数
为坐标原点,过二次函数![]() 图象上的点
图象上的点![]() ,作
,作![]() 轴的垂线交
轴的垂线交![]() 轴于点
轴于点![]() .
.
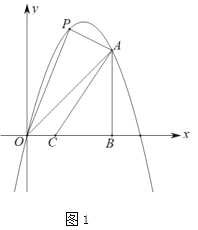
(1)如图1,![]() 为线段
为线段![]() 上方抛物线上的一点,在
上方抛物线上的一点,在![]() 轴上取点
轴上取点![]() ,点
,点![]() 、
、![]() 为
为![]() 轴上的两个动点,点
轴上的两个动点,点![]() 在点
在点![]() 的上方且
的上方且![]() 连接
连接![]() ,当四边形
,当四边形![]() 的面积最大时,求
的面积最大时,求![]() 的最小值.
的最小值.
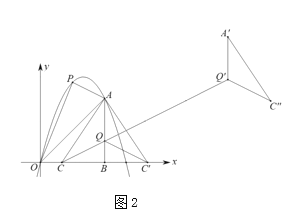
(2)如图2,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,
翻折,![]() 点的对应点为
点的对应点为![]() ,将
,将![]() 沿射线
沿射线![]() 平移
平移![]() 个单位得
个单位得![]() ,在抛物线上取一点
,在抛物线上取一点![]() ,使得以
,使得以![]() 为顶点的三角形是等腰三角形,求
为顶点的三角形是等腰三角形,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
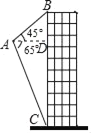
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为65°,此时航拍无人机A处与该建筑物的水平距离AD为80米.求该建筑物的高度BC(精确到1米).(参考数据:sin65°=0.91,cos65°=0.42,tan65°=2.14)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com