
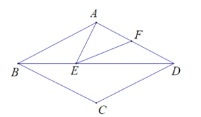
【题目】如图,菱形ABCD中,∠ABC=56°,点E,F分别在BD,AD上,当AE+EF的值最小时,则∠AEF=___度.
【答案】56
【解析】
连接AC,过点C作CF⊥AD,交BD于点E,交AD于点F,连接AE,根据菱形的性质和垂线段最短可得此时AE+EF的值最小,且最小值即为CF的长,然后根据等腰三角形的性质、直角三角形的性质和三角形外角的性质即可求出结论.
解:连接AC,过点C作CF⊥AD,交BD于点E,交AD于点F,连接AE
∵四边形ABCD为菱形,∠ABC=56°
∴菱形ABCD是以BD所在直线为对称轴的轴对称图形,∠ADC=∠ABC=56°,DA=DC
∴AE=CE,∠DAC=∠DCA=![]() (180°-∠ADC)=62°
(180°-∠ADC)=62°
∴此时AE+EF=CE+EF=CF,∠EAC=∠ECA
根据垂线段最短可知:此时AE+EF的值最小,且最小值即为CF的长
∵CF⊥AD
∴∠AFC=90°
∴∠ECA=90°-∠DAC=28°
∴∠EAC=28°
∴∠AEF=∠EAC+∠ECA=56°
故答案为:56.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
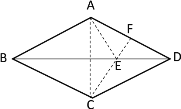
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
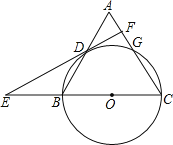
【题目】如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.
(1)求证:DF⊥AC;
(2)求tan∠E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
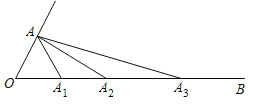
【题目】如图,已知![]() ,点
,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,点
上,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,点
上,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上….连接
上….连接![]() ,依此做法,则
,依此做法,则![]() =________,
=________,![]() =________(用含
=________(用含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂北公司以10元/千克的价格收购一批产品进行销售,为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)请你根据表中的数据确定y与x之间的函数表达式;
(2)鄂北公司应该如何确定这批产品的销售价格,才能使日销售利润W1元最大?
(3)若鄂北公司每销售1千克这种产品需支出a元(a>0)的相关费用,当20≤x≤25时,鄂北公司的日获利W2元的最大值为1215元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】外线投资是篮球队常规训练的重要项目之一,下列图表中数据是甲乙丙三从每从十次投篮测试的成绩,测试规则为连续投篮十个球为一次,投进篮筐一个球记为1分.
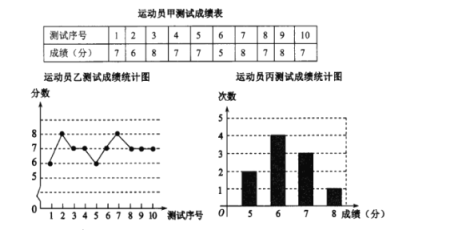
(1)写出运动员乙测试成绩的众数和中位数;
(2)在他们三从中选择一位投篮成绩优秀且较为稳定的选手作为中锋,你认为选谁更合适?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=3cm,BC=4cm,点E是BC上一点,且CE=1cm.点P由点C出发,沿CD方向向点D匀速运动,速度为1cm/s;点Q由点A出发,沿AD方向向点D匀速运动,速度为![]() cm/s,点P,Q同时出发,PQ交BD于F,连接PE,QB,设运动时间为t(s)(0<t<3).
cm/s,点P,Q同时出发,PQ交BD于F,连接PE,QB,设运动时间为t(s)(0<t<3).
(1)当t为何值时,PE∥BD?
(2)设△FQD的面积为y(cm2),求y与t之间的函数关系式.
(3)是否存在某一时刻t,使得四边形BQPE的周长最小.若存在,求出此四边形BQPE的面积;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.
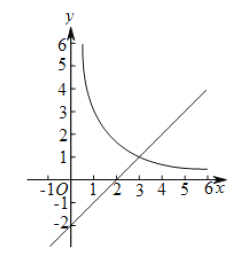
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com