
【题目】鄂北公司以10元/千克的价格收购一批产品进行销售,为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)请你根据表中的数据确定y与x之间的函数表达式;
(2)鄂北公司应该如何确定这批产品的销售价格,才能使日销售利润W1元最大?
(3)若鄂北公司每销售1千克这种产品需支出a元(a>0)的相关费用,当20≤x≤25时,鄂北公司的日获利W2元的最大值为1215元,求a的值.
【答案】(1)y=﹣15x+450;(2)这批产品的销售价格定为20元,才能使日销售利润最大;(3)a的值为2
【解析】
(1)由表格数据变化规律可知:y是x的一次函数,然后利用待定系数法求一次函数解析式即可;
(2)根据“总利润=每千克利润×千克数”即可求出W1与x的函数关系式,然后利用二次函数求最值即可;
(3)根据“总利润=每千克利润×千克数”即可求出W2与x的函数关系式,然后根据对称轴的位置分类讨论,分别求出最值,然后列出方程即可求出结论.
解:(1)由表格可知: x每增加5,y都下降75
∴y是x的一次函数
设y与x之间的函数表达式为y=kx+b,
则![]() ,
,
解得:k=﹣15,b=450,
∴y与x之间的函数表达式为:y=﹣15x+450;
(2)设日销售利润W1=y(x﹣10)=(﹣15x+450)(x﹣10)
即W1=﹣15x2+600x﹣4500
∵![]()
∴当x=﹣![]() =20时,W1有最大值1500元,
=20时,W1有最大值1500元,
答:这批产品的销售价格定为20元,才能使日销售利润最大;
(3)日获利W2=y(x﹣10﹣a)=(﹣15x+450)(x﹣10﹣a),
即W2=﹣15x2+(600+15a)x﹣(450a+4500),
则对称轴为x=20+![]() a
a
①若20+![]() a ≥25,即a≥10时,则当x=25时,W2有最大值,
a ≥25,即a≥10时,则当x=25时,W2有最大值,
即W2=1125﹣75a<1215(不合题意);
②若20<20+![]() a <25,即0<a<10时,则当x=20+
a <25,即0<a<10时,则当x=20+![]() a时,W2有最大值,
a时,W2有最大值,
将x=20+![]() a代入,可得W2=
a代入,可得W2=![]() a2﹣150a+1500,
a2﹣150a+1500,
当W2=1215时,![]() a2﹣150a+1500=1215,解得a1=2,a2=38(舍去),
a2﹣150a+1500=1215,解得a1=2,a2=38(舍去),
综上所述,a的值为2


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】为了参加西部博览会,资阳市计划印制一批宣传册.该宣传册每本共10页,由A、B两种彩页构成.已知A种彩页制版费300元/张,B种彩页制版费200元/张,共计2400元.(注:彩页制版费与印数无关)
(1)每本宣传册A、B两种彩页各有多少张?
(2)据了解,A种彩页印刷费2.5元/张,B种彩页印刷费1.5元/张,这批宣传册的制版费与印刷费的和不超过30900元.如果按到资阳展台处的参观者人手一册发放宣传册,预计最多能发给多少位参观者?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,平面直角坐标系中,直线 y1=x+3与抛物线y2=﹣![]() +2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()
+2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,线段
,线段![]() 与
与![]() 轴平行,且
轴平行,且![]() ,抛物线
,抛物线![]() (
(![]() 常数)经过点
常数)经过点![]()
(1)求![]() 的解析式及其对称轴和顶点坐标
的解析式及其对称轴和顶点坐标
(2)判断点![]() 是否在
是否在![]() 上,并说明理由;
上,并说明理由;
(3)若线段![]() 以每秒2个单位的速度向下平移,设平移的时间为
以每秒2个单位的速度向下平移,设平移的时间为![]() 秒
秒
①若![]() 与线段
与线段![]() 总有公共点,直接写出
总有公共点,直接写出![]() 的取值范围
的取值范围
②若![]() 同时以每秒3个单位的速度向下平移,
同时以每秒3个单位的速度向下平移,![]() 在
在![]() 轴及其右侧图像与直线
轴及其右侧图像与直线![]() 总有两个公共点,求
总有两个公共点,求![]() 的取值范围.
的取值范围.
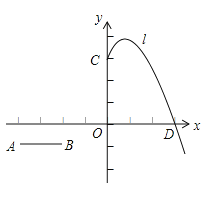
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点C、B分别在![]() 轴、
轴、![]() 轴上,△ABC是等腰直角三角形,∠BAC=90°,已知A(2,2)、P(1,0).M为BC的中点,则PM的最小值为_____.
轴上,△ABC是等腰直角三角形,∠BAC=90°,已知A(2,2)、P(1,0).M为BC的中点,则PM的最小值为_____.
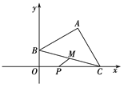
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,点P在边AB上,点D、Q分别为边BC上的点,线段AD的延长线与线段PQ的延长线交于点F,连接CP交AF于点E,若∠BPF=∠APC,FD=FQ.
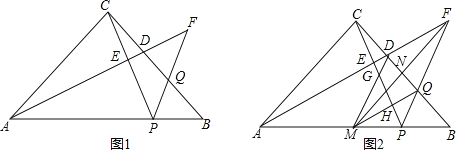
(1)如图1,求证:AF⊥CP;
(2)如图2,作∠AFP的平分线FM交AB于点M,交BC于点N,若FN=MN,求证:![]() ;
;
(3)在(2)的条件下,连接DM、MQ,分别交PC于点G、H,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明家住在30米高的A楼里,小丽家住在B楼里,B楼坐落在A楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为30°.
(1)如果A、B两楼相距16![]() 米,那么A楼落在B楼上的影子有多长?
米,那么A楼落在B楼上的影子有多长?
(2)如果A楼的影子刚好不落在B楼上,那么两楼的距离应是多少米?(结果保留根号)
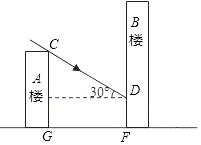
查看答案和解析>>
科目:初中数学 来源: 题型:
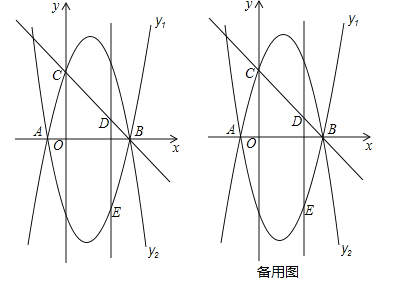
【题目】已知抛物线![]() (a≠0)与x轴交于点A(﹣1,0)和点B(4,0).
(a≠0)与x轴交于点A(﹣1,0)和点B(4,0).
(1)求抛物线![]() 的函数解析式;
的函数解析式;
(2)如图①,将抛物线![]() 沿x轴翻折得到抛物线
沿x轴翻折得到抛物线![]() ,抛物线
,抛物线![]() 与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线
与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线![]() 于点E,求线段DE的长度的最大值;
于点E,求线段DE的长度的最大值;
(3)在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线![]() 上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com