
【题目】已知,平面直角坐标系中,直线 y1=x+3与抛物线y2=﹣![]() +2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()
+2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
设过点P平行直线y1的解析式为y=x+b,当直线y=x+3与抛物线只有一个交点时,点P到直线y1的距离最小,如图设直线y1交x轴于A,交y轴于B,直线y=x+![]() 交x轴于C,作CD⊥AB于D,PE⊥AB于E,想办法求出CD的长即可解决问题.
交x轴于C,作CD⊥AB于D,PE⊥AB于E,想办法求出CD的长即可解决问题.
解:设过点P平行直线y1的解析式为y=x+b,
当直线y=x+3与抛物线只有一个交点时,点P到直线y1的距离最小,
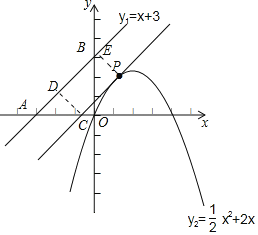
由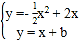 ,消去y得到:x2-2x+2b=0,
,消去y得到:x2-2x+2b=0,
当△=0时,4-8b=0,
∴b=![]() ,
,
∴直线的解析式为y=x+![]() ,
,
如图设直线y1交x轴于A,交y轴于B,直线y=x+![]() 交x轴于C,作CD⊥AB于D,PE⊥AB于E,则A(-3,0),B(0,3),C(-
交x轴于C,作CD⊥AB于D,PE⊥AB于E,则A(-3,0),B(0,3),C(-![]() ,0),
,0),
∴OA=OB=3,OC=![]() ,AC=
,AC=![]() ,
,
∴∠DAC=45°,
∴CD=![]() =
=![]() ,
,
∵AB∥PC,CD⊥AB,PE⊥AB,
∴PE=CD=![]() ,
,
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.
(1)求此抛物线的解析式;
(2)若点P是直线BC下方的抛物线上一动点(不点B,C重合),过点P作y轴的平行线交直线BC于点D,设点P的横坐标为m.
①用含m的代数式表示线段PD的长.
②连接PB,PC,求△PBC的面积最大时点P的坐标.
(3)设抛物线的对称轴与BC交于点E,点M是抛物线的对称轴上一点,N为y轴上一点,是否存在这样的点M和点N,使得以点C、E、M、N为顶点的四边形是菱形?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=50°,则∠BDE= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
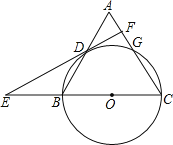
【题目】如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.
(1)求证:DF⊥AC;
(2)求tan∠E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】洛阳某科技公司生产和销售A、B两类套装电子产品![]() 已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元
已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元![]() 公司生产一套A类产品的成品是
公司生产一套A类产品的成品是![]() 万元,生产B类产品的成本如下表:
万元,生产B类产品的成本如下表:
套数 | 1 | 2 | 3 | 4 |
|
总成本 | 8 | 12 | 16 | 20 |
|
![]() 该公司A类产品和B类产品的销售单价分别是多少万元?
该公司A类产品和B类产品的销售单价分别是多少万元?
![]() ①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润
①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润![]() ________;公司销售x套B类产品的利润
________;公司销售x套B类产品的利润![]() ________.
________.
②怎样安排生产,才能使公司获得的利润较高?
查看答案和解析>>
科目:初中数学 来源: 题型:
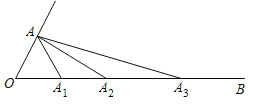
【题目】如图,已知![]() ,点
,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,点
上,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,点
上,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上….连接
上….连接![]() ,依此做法,则
,依此做法,则![]() =________,
=________,![]() =________(用含
=________(用含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂北公司以10元/千克的价格收购一批产品进行销售,为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)请你根据表中的数据确定y与x之间的函数表达式;
(2)鄂北公司应该如何确定这批产品的销售价格,才能使日销售利润W1元最大?
(3)若鄂北公司每销售1千克这种产品需支出a元(a>0)的相关费用,当20≤x≤25时,鄂北公司的日获利W2元的最大值为1215元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知在平面直角坐标系![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别为坐标轴上的三个点,且
分别为坐标轴上的三个点,且![]() ,
,![]() ,
,![]() .
.
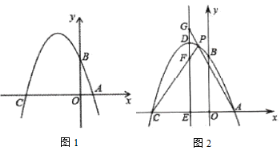
(1)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)点![]() 是抛物线上一个动点,且在直线
是抛物线上一个动点,且在直线![]() 的上方,连接
的上方,连接![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点,使四边形
,那么是否存在点,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图2,过抛物线顶点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() 、
、![]() 两点间的一个动点(点
两点间的一个动点(点![]() 不与
不与![]() 、
、![]() 两点重合),直线
两点重合),直线![]() 、
、![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 、
、![]() ,当点
,当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com