
【题目】洛阳某科技公司生产和销售A、B两类套装电子产品![]() 已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元
已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元![]() 公司生产一套A类产品的成品是
公司生产一套A类产品的成品是![]() 万元,生产B类产品的成本如下表:
万元,生产B类产品的成本如下表:
套数 | 1 | 2 | 3 | 4 |
|
总成本 | 8 | 12 | 16 | 20 |
|
![]() 该公司A类产品和B类产品的销售单价分别是多少万元?
该公司A类产品和B类产品的销售单价分别是多少万元?
![]() ①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润
①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润![]() ________;公司销售x套B类产品的利润
________;公司销售x套B类产品的利润![]() ________.
________.
②怎样安排生产,才能使公司获得的利润较高?
【答案】(1)该公司每套A类产品或B类产品的售价分别是4万元、6万元;(2)①![]() ;
;![]() ②当销售的总套数小于8套,则安排生产A类产品利润最高;当销售的总套数等于8套,则安排生产A类产品和生产B类产品利润一样;当销售的总套数大于8套,则安排生产B类产品利润最高.
②当销售的总套数小于8套,则安排生产A类产品利润最高;当销售的总套数等于8套,则安排生产A类产品和生产B类产品利润一样;当销售的总套数大于8套,则安排生产B类产品利润最高.
【解析】
![]() 通过题意联立二元一次方程方程组解得.
通过题意联立二元一次方程方程组解得.
![]() 通过利润=售价-成本便推导出,并利用不等式来解决利润最大化问题.
通过利润=售价-成本便推导出,并利用不等式来解决利润最大化问题.
解:![]() 设每套A类产品的售价是x万元,每套B类产品的售价是y万元,由题意得
设每套A类产品的售价是x万元,每套B类产品的售价是y万元,由题意得
![]() ,
,
解得![]() ,
,
答:该公司每套A类产品或B类产品的售价分别是4万元、6万元.
![]() ①∵利润=售价-成本,
①∵利润=售价-成本,
每套A类产品的售价分别是4万元,一套A类产品的成本是![]() 万元,设生产销售该类A电子产品x套,成本为
万元,设生产销售该类A电子产品x套,成本为![]() ,售价为
,售价为![]() .
.
∴![]() ;
;
∵B类产品的售价分别是6万元,成本随套数而变化,设生产销售该类B电子产品x套.
套数 | 1 | 2 | 3 | 4 |
|
总成本 | 8 | 12 | 16 | 20 |
|
由表格可得,生产B类产品1套,成本:8万元;2套,成本:12万元;3套,成本16万元;4套,20万元;……
通过观察并归纳,则成本可以代数式![]() 表示,售价为
表示,售价为![]() .
.
∴![]() .
.
②当![]() 时,有
时,有![]() ,解得
,解得![]() ;
;
当![]() 时,有
时,有![]() ,解得
,解得![]() ;
;
当![]() 时,有
时,有![]() ,解得
,解得![]() .
.
综上所述,当销售的总套数小于8套,则安排生产A类产品利润最高;
当销售的总套数等于8套,则安排生产A类产品和生产B类产品利润一样;
当销售的总套数大于8套,则安排生产B类产品利润最高.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF.其中正确的结论有( )个
S△ABF.其中正确的结论有( )个
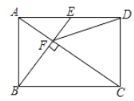
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 中,
中,![]() 为
为![]() 内一点,将
内一点,将![]() 绕点
绕点![]() 按逆时针方向旋转角
按逆时针方向旋转角![]() 得到
得到![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]() ,且
,且![]() 三点在同一直线上.
三点在同一直线上.
(1)填空:![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)如图2,若![]() ,请补全图形,再过点
,请补全图形,再过点![]() 作
作![]() 于点
于点![]() ,然后探究线段
,然后探究线段![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(3)若![]() ,且点
,且点![]() 满足
满足![]() ,直接写出点
,直接写出点![]() 到
到![]() 的距离.
的距离.
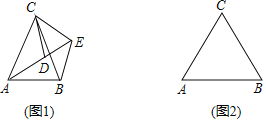
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与两轴分别交于A、B、C三点,已知点A(﹣3,0),B(1,0).点P在第二象限内的抛物线上运动,作PD⊥x轴于点D,交直线AC于点E.
(1)b= ;c= ;
(2)求线段PE取最大值时点P的坐标,这个最大值是多少;
(3)连接AP,并以AP为边作等腰直角△APQ,当顶点Q恰好落在抛物线的对称轴上时,直接写出对应的P点坐标.
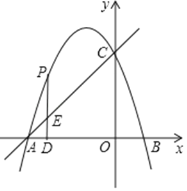
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,平面直角坐标系中,直线 y1=x+3与抛物线y2=﹣![]() +2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()
+2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系,根据图象解决以下问题:
(1)慢车的速度为_____km/h,快车的速度为_____km/h;
(2)解释图中点C的实际意义并求出点C的坐标;
(3)求当x为多少时,两车之间的距离为500km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,线段
,线段![]() 与
与![]() 轴平行,且
轴平行,且![]() ,抛物线
,抛物线![]() (
(![]() 常数)经过点
常数)经过点![]()
(1)求![]() 的解析式及其对称轴和顶点坐标
的解析式及其对称轴和顶点坐标
(2)判断点![]() 是否在
是否在![]() 上,并说明理由;
上,并说明理由;
(3)若线段![]() 以每秒2个单位的速度向下平移,设平移的时间为
以每秒2个单位的速度向下平移,设平移的时间为![]() 秒
秒
①若![]() 与线段
与线段![]() 总有公共点,直接写出
总有公共点,直接写出![]() 的取值范围
的取值范围
②若![]() 同时以每秒3个单位的速度向下平移,
同时以每秒3个单位的速度向下平移,![]() 在
在![]() 轴及其右侧图像与直线
轴及其右侧图像与直线![]() 总有两个公共点,求
总有两个公共点,求![]() 的取值范围.
的取值范围.
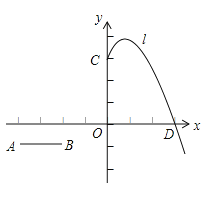
查看答案和解析>>
科目:初中数学 来源: 题型:
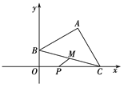
【题目】在平面直角坐标系中,点C、B分别在![]() 轴、
轴、![]() 轴上,△ABC是等腰直角三角形,∠BAC=90°,已知A(2,2)、P(1,0).M为BC的中点,则PM的最小值为_____.
轴上,△ABC是等腰直角三角形,∠BAC=90°,已知A(2,2)、P(1,0).M为BC的中点,则PM的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() .
.
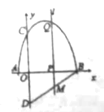
(1)求点![]() 、点
、点![]() 、点
、点![]() 的坐标;
的坐标;
(2)当点![]() 在线段
在线段![]() 上运动时,直线
上运动时,直线![]() 交
交![]() 于点
于点![]() ,试探究当
,试探究当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)在点![]() 的运动过程中,是否存在点
的运动过程中,是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com