
����Ŀ����ͼ����֪������y��ax2+bx+3��a��0��������A(1��0)�͵�B(3��0)����y�ύ�ڵ�C��
��1����������ߵĽ���ʽ��
��2������P��ֱ��BC�·�����������һ���㣨����B��C�غϣ�������P��y���ƽ���߽�ֱ��BC�ڵ�D�����P�ĺ�����Ϊm��
���ú�m�Ĵ���ʽ��ʾ�߶�PD�ij���
������PB��PC������PBC��������ʱ��P�����꣮
��3���������ߵĶԳ�����BC���ڵ�E����M�������ߵĶԳ�����һ�㣬NΪy����һ�㣬�Ƿ���������ĵ�M�͵�N��ʹ���Ե�C��E��M��NΪ������ı��������Σ�������ڣ���ֱ��д����M�����ꣻ��������ڣ���˵�����ɣ�

���𰸡���1��y��x2��4x+3����2���٩�m2+3m����(![]() ����
����![]() )����3�����ڣ���M������Ϊ(2��3)��( 2��1��2
)����3�����ڣ���M������Ϊ(2��3)��( 2��1��2![]() )��(2��1+2
)��(2��1+2![]() )
)
��������
��1��������֪������y=ax2+bx+3��a��0��������A��1��0���͵�B��3��0�����뼴����⣻
��2������ȷ��ֱ��BC����ʽ�����ݹ���P��y���ƽ���߽�ֱ��BC�ڵ�D�������ú�m�Ĵ������ʾ��P��D�����������⣻
���ú�m�Ĵ���ʽ��ʾ����PBC��������ɵ�S�ǹ���m�Ķ��κ�����������⣻
��3�����ݣ�1�������ö��κ���ͼ��ͶԳ����ȵõ�E�����꼴��д��������λ�õĵ�M�����꣮
�⣺��1����������y��ax2+bx+3��a��0��������A��1��0���͵�B��3��0������y�ύ�ڵ�C��
��![]() ��
��
��ã�![]() ��
��
�������߽���ʽΪ��y��x2��4x+3��
��2����ͼ��
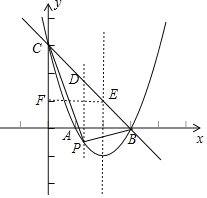
����P��m��m2��4m+3����
����B��3��0����C��0��3�������ֱ��BC����ʽΪyBC����x+3��
�߹���P��y���ƽ���߽�ֱ��BC�ڵ�D��
��D��m����m+3����
��PD������m+3������m2��4m+3������m2+3m��
���ú�m�Ĵ���ʽ��ʾ�߶�PD�ij�Ϊ��m2+3m��
��S��PBC��S��CPD+S��BPD
��![]() OBPD����
OBPD����![]() m2+
m2+![]() m
m
����![]() ��m��
��m��![]() ��2+
��2+![]() ��
��
�൱m��![]() ʱ��S�����ֵ��
ʱ��S�����ֵ��
��m��![]() ʱ��m2��4m+3����
ʱ��m2��4m+3����![]() ��
��
��P��![]() ����
����![]() ����
����
����PBC��������ʱ��P������Ϊ��![]() ����
����![]() ����
����
��3�����������ĵ�M�͵�N��ʹ���Ե�C��E��M��NΪ������ı��������Σ�
�������⣬��E��2��1����
��EF��CF��2��
��EC��![]() ��
��
�������ε���������ȣ�
��ME��EC��![]() ��
��
��M��2��1��![]() ����2��1+
����2��1+![]() ��
��
��EM��EF��2ʱ��M��2��3��
���M������ΪM1��2��3����M2��2��1��2![]() ����M3��2��1+2
����M3��2��1+2![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
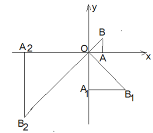
����Ŀ����ͼ,��ƽ�������ϵxOy��,��һ������ֱ�������Ρ�AOB,��OAB=90��,ֱ�DZ�AO��x���ϣ���AO=1,��Rt��AOB��ԭ��O˳ʱ����ת90�����ٽ����߳�����һ�����õ�����ֱ��������A1OB1;��Rt��A1OB1��ԭ��O˳ʱ��ת90�����ٽ����߳�����һ�����õ�����������A2OB2......���˹��ɣ��õ�����ֱ��������A2017OB2017�����B2017������_________ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�����ϵĴ�˵����һ���������ø������������õ���ˡ�Ļ��ᣮ���������룬һ������װ��5��������һ������װ�ų���ɫ��ͬ��������һ����5�����������۾����ţ�Ȼ��Ҫѡ��һ���룬���������ó�һ����������õ��Ǻ����Ҫ�������ڼ������棬������õ��ǰ��ͽ�������ɣ�����ס�۾�֮ǰ�����������ϣ����·�װ���������ڣ��������������Բ�ͬ������������һ�����������ô����ʹ���Լ�������ɵĻ���������˻�����ɵ��������ǣ�������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲μ����������ᣬ�����мƻ�ӡ��һ�������ᣮ��������ÿ����10ҳ����A��B���ֲ�ҳ���ɣ���֪A�ֲ�ҳ�ư��300Ԫ/�ţ�B�ֲ�ҳ�ư��200Ԫ/�ţ�����2400Ԫ����ע����ҳ�ư����ӡ���أ�
��1��ÿ��������A��B���ֲ�ҳ���ж����ţ�
��2�����˽⣬A�ֲ�ҳӡˢ��2.5Ԫ/�ţ�B�ֲ�ҳӡˢ��1.5Ԫ/�ţ�������������ư����ӡˢ�ѵĺͲ�����30900Ԫ�������������չ̨���IJι�������һ�ᷢ�������ᣬԤ������ܷ�������λ�ι��ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
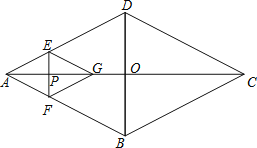
����Ŀ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AC��16��BD��12������P���߶�AC�ϴӵ�A���C��4����λ/����ٶ��˶�������P��EF��AC��������ABCD�ı��ڵ�E��F����ֱ��AC����һ��G��ʹ��AEF����GEF����EF�Գƣ�������ABCD���ı���AEGF��ס���ֵ����ΪS1��δ����ס���ֵ����ΪS2����P�˶�ʱ��Ϊx�룮
��1���ú�x�Ĵ���ʽ�ֱ��ʾS1��S2��
��2����S1��S2����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��![]() �У�
�У�![]() Ϊ
Ϊ![]() ��һ�㣬��
��һ�㣬��![]() �Ƶ�
�Ƶ�![]() ����ʱ�뷽����ת��
����ʱ�뷽����ת��![]() �õ�
�õ�![]() ����
����![]() �Ķ�Ӧ��ֱ�Ϊ��
�Ķ�Ӧ��ֱ�Ϊ��![]() ����
����![]() ������ͬһֱ���ϣ�
������ͬһֱ���ϣ�
��1����գ�![]() �� �����ú�
�� �����ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2����ͼ2����![]() ���벹ȫͼ�Σ��ٹ���
���벹ȫͼ�Σ��ٹ���![]() ��
��![]() �ڵ�
�ڵ�![]() ��Ȼ��̽���߶�
��Ȼ��̽���߶�![]() ֮���������ϵ����֤����Ľ��ۣ�
֮���������ϵ����֤����Ľ��ۣ�
��3����![]() ���ҵ�
���ҵ�![]() ����
����![]() ��ֱ��д����
��ֱ��д����![]() ��
��![]() �ľ��룮
�ľ��룮
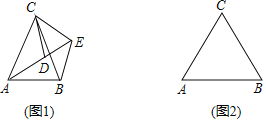
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ֽƬABCD�У�AB��8��AD��17���۵�ֽƬʹ��B���ڱ�AD�ϵ�E�����ۺ�ΪPQ����E��AD�����ƶ�ʱ���ۺ۵Ķ˵�P��QҲ�����ƶ�������P��Q�ֱ��ڱ�BA��BC���ƶ������E�ڱ�AD���ƶ���������Ϊ��������
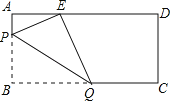
A.6B.7C.8D.9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ�У�ֱ�� y1=x+3��������y2=��![]() +2x ��ͼ����ͼ����P�� y2 �ϵ�һ�����㣬���P��ֱ�� y1 ����̾���Ϊ����
+2x ��ͼ����ͼ����P�� y2 �ϵ�һ�����㣬���P��ֱ�� y1 ����̾���Ϊ����

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���ACB=90����AC=BC����P�ڱ�AB�ϣ���D��Q�ֱ�Ϊ��BC�ϵĵ㣬�߶�AD���ӳ������߶�PQ���ӳ��߽��ڵ�F������CP��AF�ڵ�E������BPF=��APC��FD=FQ��
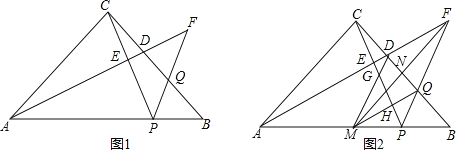
��1����ͼ1����֤��AF��CP��
��2����ͼ2������AFP��ƽ����FM��AB�ڵ�M����BC�ڵ�N����FN=MN����֤��![]() ��
��
��3���ڣ�2���������£�����DM��MQ���ֱ�PC�ڵ�G��H����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com