
【题目】在△ABC中,∠ACB=90°,AC=BC,点P在边AB上,点D、Q分别为边BC上的点,线段AD的延长线与线段PQ的延长线交于点F,连接CP交AF于点E,若∠BPF=∠APC,FD=FQ.
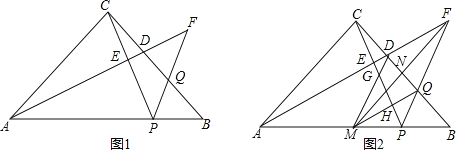
(1)如图1,求证:AF⊥CP;
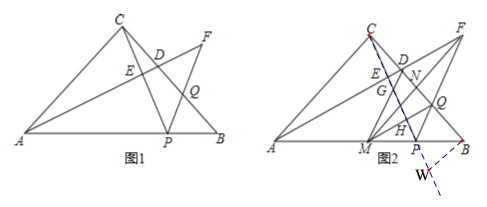
(2)如图2,作∠AFP的平分线FM交AB于点M,交BC于点N,若FN=MN,求证:![]() ;
;
(3)在(2)的条件下,连接DM、MQ,分别交PC于点G、H,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)由∠APC=∠BPQ,得∠ACP=∠PQB,由∠FDQ=∠CDA,∠FQD=∠PQB,推出∠ACP=∠CDA,由∠ACP=∠CDA,推出CP⊥AF;
(2)作WB⊥BC,交CP延长线于点W,由△ACD≌△CBW,QBPWBP,得出CD=QB,由FM平分∠DFQ,DF=FQ,,得到 ND=NQ,FN⊥BC,
由MN=FN=![]() ,得到 DN=
,得到 DN=![]() DC,由DN=NQ,得到DQ=
DC,由DN=NQ,得到DQ=![]() BC;
BC;
(3)易证四边形DFQM是平行四边形,进而得△EDG~△HQP,即可求解.
(1)∵∠APC=∠BPQ,∠A=∠B,∠APC+∠A+∠ACP=∠BPQ+∠B+∠PQB=180°,
∴∠ACP=∠PQB,
∵FD=FQ,
∴∠FQD=∠FDQ,
又∵∠FDQ=∠CDA, ∠FQD=∠PQB,
∴∠CDA=∠PQB,
∴∠ACP=∠CDA,
∴∠CDA +∠BCP =∠ACP+∠BCP=∠ACB=90°,
∴AF⊥CP;
(2)作WB⊥BC,交CP延长线于点W,
∵∠ABC=∠PBW=45°,PB=PB,∠BPF=∠APC=∠BPW,
∴QBPWBP(ASA),
∴BQ=BW,
∵∠BCP+∠ACP=∠ACP+∠CAD=90°,
∴∠BCP=∠CAD,
∵AC=BC,∠ACD=∠CBW=90°,
∴ACDCBW(ASA),
∴CD=BW,
∴BQ= CD,
∵FM平分∠DFQ,DF=FQ,
∴ ND=NQ,FN⊥BC,
∴FN∥AC,
∵CD+DN=BQ+QN,
∴CN=BN,
∴MN是BAC的中位线,
∴MN=FN=![]() ,
,
∴![]() ,即:DN=
,即:DN=![]() ,
,
∴DN=NQ=![]() =
=![]() ,
,
∴DQ= CD=BQ,
∴DQ=![]() BC;
BC;
(3)∵DN=NQ,MN=FN,
∴四边形DFQM是平行四边形,
∴AF∥MQ,DM∥FP,
∴∠EGD=∠HPQ,∠DEG=∠QHP=90°,
∴△EDG~△HQP ,
∴![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.
(1)求此抛物线的解析式;
(2)若点P是直线BC下方的抛物线上一动点(不点B,C重合),过点P作y轴的平行线交直线BC于点D,设点P的横坐标为m.
①用含m的代数式表示线段PD的长.
②连接PB,PC,求△PBC的面积最大时点P的坐标.
(3)设抛物线的对称轴与BC交于点E,点M是抛物线的对称轴上一点,N为y轴上一点,是否存在这样的点M和点N,使得以点C、E、M、N为顶点的四边形是菱形?如果存在,请直接写出点M的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
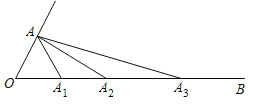
【题目】如图,已知![]() ,点
,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,点
上,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,点
上,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上….连接
上….连接![]() ,依此做法,则
,依此做法,则![]() =________,
=________,![]() =________(用含
=________(用含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂北公司以10元/千克的价格收购一批产品进行销售,为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)请你根据表中的数据确定y与x之间的函数表达式;
(2)鄂北公司应该如何确定这批产品的销售价格,才能使日销售利润W1元最大?
(3)若鄂北公司每销售1千克这种产品需支出a元(a>0)的相关费用,当20≤x≤25时,鄂北公司的日获利W2元的最大值为1215元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】外线投资是篮球队常规训练的重要项目之一,下列图表中数据是甲乙丙三从每从十次投篮测试的成绩,测试规则为连续投篮十个球为一次,投进篮筐一个球记为1分.
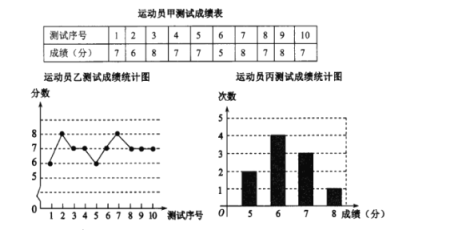
(1)写出运动员乙测试成绩的众数和中位数;
(2)在他们三从中选择一位投篮成绩优秀且较为稳定的选手作为中锋,你认为选谁更合适?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子中装有2个红球,1个白球和1个蓝球,这些球除颜色外都相同,小明和小凡准备用这些球做游戏,游戏规则如下:从盒子中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,若两次摸到的球的颜色都是红色,小明胜;若两次摸到的球的颜色能配成紫色,则小凡胜,这个游戏对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=3cm,BC=4cm,点E是BC上一点,且CE=1cm.点P由点C出发,沿CD方向向点D匀速运动,速度为1cm/s;点Q由点A出发,沿AD方向向点D匀速运动,速度为![]() cm/s,点P,Q同时出发,PQ交BD于F,连接PE,QB,设运动时间为t(s)(0<t<3).
cm/s,点P,Q同时出发,PQ交BD于F,连接PE,QB,设运动时间为t(s)(0<t<3).
(1)当t为何值时,PE∥BD?
(2)设△FQD的面积为y(cm2),求y与t之间的函数关系式.
(3)是否存在某一时刻t,使得四边形BQPE的周长最小.若存在,求出此四边形BQPE的面积;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知在平面直角坐标系![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别为坐标轴上的三个点,且
分别为坐标轴上的三个点,且![]() ,
,![]() ,
,![]() .
.
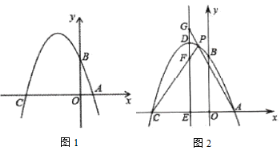
(1)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)点![]() 是抛物线上一个动点,且在直线
是抛物线上一个动点,且在直线![]() 的上方,连接
的上方,连接![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点,使四边形
,那么是否存在点,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图2,过抛物线顶点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() 、
、![]() 两点间的一个动点(点
两点间的一个动点(点![]() 不与
不与![]() 、
、![]() 两点重合),直线
两点重合),直线![]() 、
、![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 、
、![]() ,当点
,当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
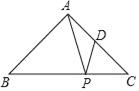
【题目】如图,在等腰直角三角形ABC中,AB=AC=2,∠BAC=90°,点D是AC的中点,点P是BC边上的动点,连接PA、PD.则PA+PD的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com