
【题目】如图,在等腰直角三角形ABC中,AB=AC=2,∠BAC=90°,点D是AC的中点,点P是BC边上的动点,连接PA、PD.则PA+PD的最小值为( )
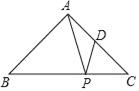
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,点P在边AB上,点D、Q分别为边BC上的点,线段AD的延长线与线段PQ的延长线交于点F,连接CP交AF于点E,若∠BPF=∠APC,FD=FQ.
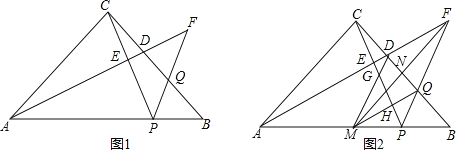
(1)如图1,求证:AF⊥CP;
(2)如图2,作∠AFP的平分线FM交AB于点M,交BC于点N,若FN=MN,求证:![]() ;
;
(3)在(2)的条件下,连接DM、MQ,分别交PC于点G、H,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过原点O的抛物线![]() (a≠0)与x轴交于另一点A(
(a≠0)与x轴交于另一点A(![]() ,0),在第一象限内与直线y=x交于点B(2,t).
,0),在第一象限内与直线y=x交于点B(2,t).
(1)求这条抛物线的表达式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
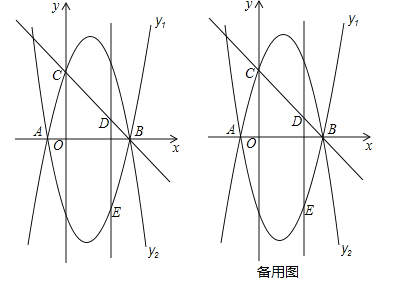
【题目】已知抛物线![]() (a≠0)与x轴交于点A(﹣1,0)和点B(4,0).
(a≠0)与x轴交于点A(﹣1,0)和点B(4,0).
(1)求抛物线![]() 的函数解析式;
的函数解析式;
(2)如图①,将抛物线![]() 沿x轴翻折得到抛物线
沿x轴翻折得到抛物线![]() ,抛物线
,抛物线![]() 与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线
与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线![]() 于点E,求线段DE的长度的最大值;
于点E,求线段DE的长度的最大值;
(3)在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线![]() 上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
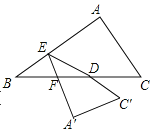
【题目】如图,在Rt△ABC中,AC=3,AB=4,D为斜边BC的中点,E为AB上一个动点,将△ABC沿直线DE折叠,A,C的对应点分别为![]() ,
,![]() ,
,![]() 交BC于点F,若△BEF为直角三角形,则BE的长度为______.
交BC于点F,若△BEF为直角三角形,则BE的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了接受“省艺术特色学校”的验收,对义务教育的七、八、九三个年级学生举行了书法大赛,赛后对三个年级的获奖情况进行了统计,并绘制了如图所示的两幅不完整的统计图.
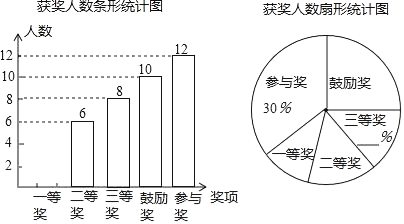
请解答下列问题:
(1)请补全两幅统计图;
(2)获得一等奖的同学有![]() 来自七年级,有
来自七年级,有![]() 来自八年级,其余同学均来自九年级.现准备从获得一等奖的同学中任选两人参加市内书法大赛,请你通过列表或画树状图,求所选两人中既有八年级同学又有九年级同学的概率.
来自八年级,其余同学均来自九年级.现准备从获得一等奖的同学中任选两人参加市内书法大赛,请你通过列表或画树状图,求所选两人中既有八年级同学又有九年级同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将大小相同的正三角形按如图所示的规律拼图案,其中第①个图案中有6个小三角形和1个正六边形;第②个图案中有10个小三角形和2个正六边形;第③个图案中有14个小三角形和3个正六边形;…;按此规律排列下去,已知一个小三角形的面积为a,一个正六边形的面积为b,则第⑧个图案中所有的小三角形和正六边形的面积之和为____________.(结果用含a、b的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:其中正确的个数是( )
,1),下列结论:其中正确的个数是( )
①a<0;
②b<0;
③c<0;
④![]() ;
;
⑤a+b+c<0.
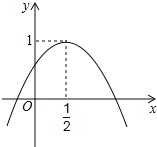
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2-
x2-![]() x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.

(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com