练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，二次函数y＝ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为（，1），下列结论：其中正确的个数是（　　）

    ①a＜0；

    ②b＜0；

    ③c＜0；

    ④；

    ⑤a+b+c＜0．

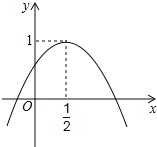
    A.1 个B.2 个C.3 个D.4 个

    【答案】B

    【解析】

    根据二次函数图象的开口方向、对称轴位置、与x轴、y轴的交点坐标、过（1，a+b+c）等知识，逐个判断即可．

    解：抛物线开口向下，因此①正确，

    对称轴为x＝＞0，可知a、b异号，a＜0，则b＞0，因此②不正确；

    抛物线与y轴交点在正半轴，因此c＞0，故③不正确；

    抛物线的顶点坐标为（﹣，），又顶点坐标为（，1），因此④正确；

    抛物线与x轴的一个交点在x轴的负半轴，对称轴为x＝，

    当x＝1时，y＝a+b+c＞0，因此⑤不正确；

    综上所述，正确的结论有2个，

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，已知在平面直角坐标系中，点、、分别为坐标轴上的三个点，且，，．

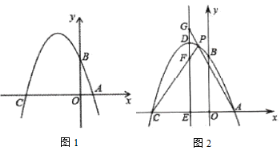
    （1）求经过、、三点的抛物线的解析式；

    （2）点是抛物线上一个动点，且在直线的上方，连接、，并把沿翻折，得到四边形，那么是否存在点，使四边形为菱形？若存在，请求出此时点的坐标；若不存在，请说明理由；

    （3）如图2，过抛物线顶点作直线轴，交轴于点，点是抛物线上、两点间的一个动点（点不与、两点重合），直线、与直线分别交于点、，当点运动时，是否为定值？若是，试求出该定值；若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰直角三角形ABC中，AB＝AC＝2，∠BAC＝90°，点D是AC的中点，点P是BC边上的动点，连接PA、PD．则PA+PD的最小值为（　　）

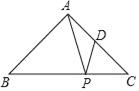
    A.B.C.D.3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

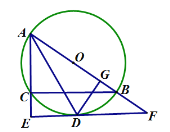
    【题目】如图，⊙O是△ABC的外接圆，AB为⊙O的直径，过点A作AD平分∠BAC交⊙O于点D，过点D作BC的平行线分别交AC、AB的延长线于点E、F，DG⊥AB于点G，连接BD．

    (1)求证：△AED∽△DGB；

    (2)求证：EF是⊙O的切线；

    (3)若，OA＝4，求劣弧的长度(结果保留π)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小帆同学根据函数的学习经验，对函数进行探究，已知函数过，，．

    （1）求函数解析式；

    （2）如图1，在平面直角坐标系中画的图象，根据函数图象，写出函数的一条性质　　　　；

    （3）结合函数图象回答下列问题：

    ①方程的近似解的取值范围(精确到个位)是　　　　；

    ②若一次函数与有且仅有两个交点，则的取值范围是　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

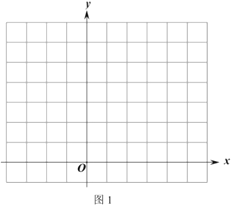
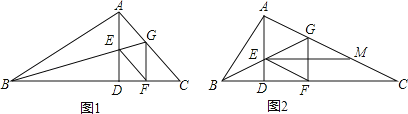
    【题目】在△ABC中，∠BAC＝90°，AD⊥BC于D，BG平分∠ABC交AD于E，交AC于G，GF⊥BC于F，连接EF．

    （1）如图1，求证：四边形AEFG是菱形；

    （2）如图2，若E为BG的中点，过点E作EM∥BC交AC于M，在不添加任何辅助线的情况下，请直接写出图2中是CM长倍的所有线段．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AC平分∠BCD，AC⊥AB，E是BC的中点，AD⊥AE．

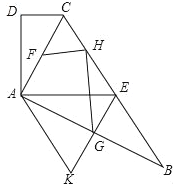
    （1）求证：AC2=CD·BC；

    （2）过E作EG⊥AB，并延长EG至点K，使EK=EB．

    ①若点H是点D关于AC的对称点，点F为AC的中点，求证：FH⊥GH；

    ②若∠B=30°，求证：四边形AKEC是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB是圆O的直径，弦CD⊥AB，垂足为H，与AC平行的圆O的一条切线交CD的延长线于点M，交AB的延长线于点E，切点为F，连接AF交CD于点N．

    （1）求证：CA=CN；

    （2）连接DF，若cos∠DFA=，AN=，求圆O的直径的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某种型号的温控水箱的工作过程是：接通电源后，在初始温度20℃下加热水箱中的水；当水温达到设定温度80℃时，加热停止；此后水箱中的水温开始逐渐下降，当下降到20℃时，再次自动加热水箱中的水至80℃时，加热停止；当水箱中的水温下降到20℃时，再次自动加热，…，按照以上方式不断循环．

    小明根据学习函数的经验，对该型号温控水箱中的水温随时间变化的规律进行了探究．发现水温y是时间x的函数，其中y（单位：℃）表示水箱中水的温度．x（单位：min）表示接通电源后的时间．

    下面是小明的探究过程，请补充完整：

    （1）下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况

    接通电源后的时间x（单位：min）

    0

    1

    2

    3

    4

    5

    8

    10

    16

    18

    20

    21

    24

    32

    …

    水箱中水的温度y（单位：℃）

    20

    35

    50

    65

    80

    64

    40

    32

    20

    m

    80

    64

    40

    20

    …

    m的值为 ；

    （2）①当0≤x≤4时，写出一个符合表中数据的函数解析式 ；

    当4＜x≤16时，写出一个符合表中数据的函数解析式 ；

    ②如图，在平面直角坐标系xOy中，描出了上表中部分数据对应的点，根据描出的点，画出当0≤x≤32时，温度y随时间x变化的函数图象：

    （3）如果水温y随时间x的变化规律不变，预测水温第8次达到40℃时，距离接通电源 min．

    查看答案和解析>>

    同步练习册答案