
【题目】小帆同学根据函数的学习经验,对函数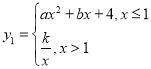 进行探究,已知函数过
进行探究,已知函数过![]() ,
,![]() ,
,![]() .
.
(1)求函数![]() 解析式;
解析式;
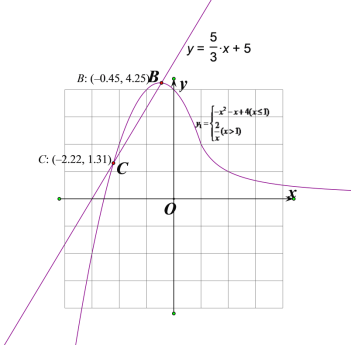
(2)如图1,在平面直角坐标系中画![]() 的图象,根据函数图象,写出函数的一条性质 ;
的图象,根据函数图象,写出函数的一条性质 ;
(3)结合函数图象回答下列问题:
①方程![]() 的近似解的取值范围(精确到个位)是 ;
的近似解的取值范围(精确到个位)是 ;
②若一次函数![]() 与
与![]() 有且仅有两个交点,则
有且仅有两个交点,则![]() 的取值范围是 .
的取值范围是 .
【答案】(1)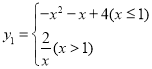 ;(2)图象见详解,当
;(2)图象见详解,当![]() 时,函数
时,函数![]() 有最大值
有最大值![]() ,函数
,函数![]() 无最小值;(3)①
无最小值;(3)①![]() 或
或![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)根据待定系数法,即可求解;
(2)画出反比例函数图象和二次函数的图象,即可得到函数的性质;
(3)①画出函数y1与y=![]() 的图象,它们的交点的横坐标,就是方程
的图象,它们的交点的横坐标,就是方程![]() 的解,进而即可得到解的取值范围;
的解,进而即可得到解的取值范围;
②结合一次函数![]() 与
与![]() 的图象,即可求解.
的图象,即可求解.
(1)将点![]() ,
,![]() 代入
代入![]() ,
,
可得![]() ,解得
,解得![]() ,
,
∴![]() ,
,
将点![]() 代入
代入![]() ,
,
可得![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∴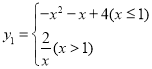 ;
;
(2)函数图象如图所示,由图象可知:当![]() 时,函数
时,函数![]() 有最大值
有最大值![]() ,函数
,函数![]() 无最小值,
无最小值,
故答案是:当![]() 时,函数
时,函数![]() 有最大值
有最大值![]() ,函数
,函数![]() 无最小值;
无最小值;
(3)①画出y=![]() 的图象,可得函数y1与y=
的图象,可得函数y1与y=![]() 的图象的交点位置,如图所示,
的图象的交点位置,如图所示,
∴方程![]() 的近似解的取值范围(精确到个位)是:
的近似解的取值范围(精确到个位)是:![]() 或
或![]() ,
,
故答案是:![]() 或
或![]() ;
;
②由题意可知:![]() 的图象过点(0,2),
的图象过点(0,2),
当k>0时,一次函数![]() 与
与![]() 有且仅有两个交点,
有且仅有两个交点,
当![]() 的图象与
的图象与![]() 的图象相切时,一次函数
的图象相切时,一次函数![]() 与
与![]() 有且仅有两个交点,
有且仅有两个交点,
∴![]() =
=![]() 有两个相等的根,即:=
有两个相等的根,即:=![]() ,
,
∴k=![]() ,
,
综上所述:![]() 或
或![]() .
.
故答案是:![]() 或
或![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案科目:初中数学 来源: 题型:
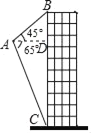
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为65°,此时航拍无人机A处与该建筑物的水平距离AD为80米.求该建筑物的高度BC(精确到1米).(参考数据:sin65°=0.91,cos65°=0.42,tan65°=2.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
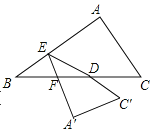
【题目】如图,在Rt△ABC中,AC=3,AB=4,D为斜边BC的中点,E为AB上一个动点,将△ABC沿直线DE折叠,A,C的对应点分别为![]() ,
,![]() ,
,![]() 交BC于点F,若△BEF为直角三角形,则BE的长度为______.
交BC于点F,若△BEF为直角三角形,则BE的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将大小相同的正三角形按如图所示的规律拼图案,其中第①个图案中有6个小三角形和1个正六边形;第②个图案中有10个小三角形和2个正六边形;第③个图案中有14个小三角形和3个正六边形;…;按此规律排列下去,已知一个小三角形的面积为a,一个正六边形的面积为b,则第⑧个图案中所有的小三角形和正六边形的面积之和为____________.(结果用含a、b的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
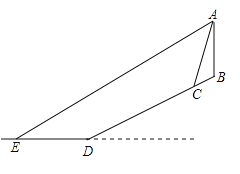
【题目】寒假期间,小明和好朋友一起前往三亚旅游.他们租住的宾馆![]() 坐落在坡度为
坐落在坡度为![]() 的斜坡上.宾馆
的斜坡上.宾馆![]() 高为129米.某天,小明在宾馆顶楼的海景房
高为129米.某天,小明在宾馆顶楼的海景房![]() 处向外看风景,发现宾馆前有一座雕像
处向外看风景,发现宾馆前有一座雕像![]() (雕像的高度忽略不计),已知雕像
(雕像的高度忽略不计),已知雕像![]() 距离海岸线
距离海岸线![]() 的距离
的距离![]() 为260米,与宾馆
为260米,与宾馆![]() 的水平距离为36米,远处海面上一艘即将靠岸的轮船
的水平距离为36米,远处海面上一艘即将靠岸的轮船![]() 的俯角为
的俯角为![]() .则轮船
.则轮船![]() 距离海岸线
距离海岸线![]() 的距离
的距离![]() 的长为( )
的长为( )
(参考数据:![]() ,
,![]() )
)
A.262米B.212米C.244米D.276米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:其中正确的个数是( )
,1),下列结论:其中正确的个数是( )
①a<0;
②b<0;
③c<0;
④![]() ;
;
⑤a+b+c<0.
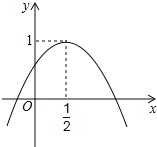
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
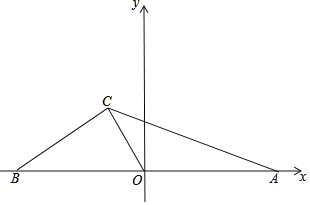
【题目】如图,在平面直角坐标系中,直线BC:y=![]() 交x轴于点B,点A在x轴正半轴上,OC为△ABC的中线,C的坐标为(m,
交x轴于点B,点A在x轴正半轴上,OC为△ABC的中线,C的坐标为(m,![]() )
)
(1)求线段CO的长;
(2)点D在OC的延长线上,连接AD,点E为AD的中点,连接CE,设点D的横坐标为t,△CDE的面积为S,求S与t的函数解析式;
(3)在(2)的条件下,点F为射线BC上一点,连接DB、DF,且∠FDB=∠OBD,CE=![]() ,求此时S值及点F坐标.
,求此时S值及点F坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
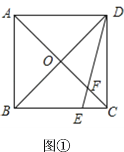
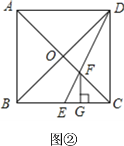
【题目】如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.
(1)如图①,当![]() 时,求
时,求![]() 的值;
的值;
(2)如图②,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=![]() BG.
BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
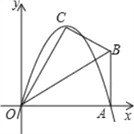
【题目】已知在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形,若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com