
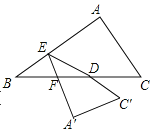
【题目】如图,在Rt△ABC中,AC=3,AB=4,D为斜边BC的中点,E为AB上一个动点,将△ABC沿直线DE折叠,A,C的对应点分别为![]() ,
,![]() ,
,![]() 交BC于点F,若△BEF为直角三角形,则BE的长度为______.
交BC于点F,若△BEF为直角三角形,则BE的长度为______.
【答案】![]() 或
或![]() .
.
【解析】
根据∠B为锐角,分两种情况进行讨论:当∠BEF=90°时,△BEF为直角三角形;当∠BFE=90°时,△BEF为直角三角形,分别根据等腰直角三角形的性质,三角形中位线定理,轴对称的性质以及直角三角形的边角关系进行计算,即可得到BE的长度.
解:分两种情况:
①如图,当∠BEF=90°时,△BEF为直角三角形,
过D作DM⊥AB于M,则∠EMD=90°,DM∥AC,
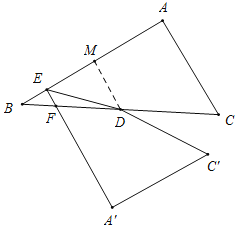
∵D为BC的中点,
∴M为AB的中点,
![]() ,
,
由折叠可得,![]() ,
,
∴△DEM是等腰直角三角形,
![]() ,
,
![]() ;
;
②如图,当∠BFE=90°时,△BEF为直角三角形,
连接AD,A'D,
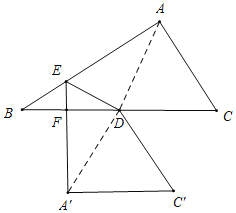
根据对称性可得,∠EAD=∠EA'D,AD=A'D
∵Rt△ABC中,AC=3,AB=4,
∴BC=5,
∵Rt△ABC中,D为BC的中点,
![]() ,
,
∴∠B=∠EAD,
∴∠B=∠FA'D,
设BE=x,则![]() ,
,
![]() ,
,
又∵Rt△A'DF中,sin∠FA'D=sinB,即![]() ,
,
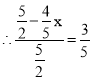 ,
,
解得![]() ,
,
即![]() ,
,
综上所述,BE的长度为![]() 或
或![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】外线投资是篮球队常规训练的重要项目之一,下列图表中数据是甲乙丙三从每从十次投篮测试的成绩,测试规则为连续投篮十个球为一次,投进篮筐一个球记为1分.
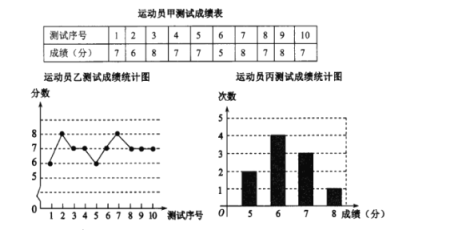
(1)写出运动员乙测试成绩的众数和中位数;
(2)在他们三从中选择一位投篮成绩优秀且较为稳定的选手作为中锋,你认为选谁更合适?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点
的图象过点![]() 且与直线
且与直线![]() 相交于
相交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上.
轴上.
![]() 求二次函数的解析式.
求二次函数的解析式.
![]() 如果
如果![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 为坐标原点,试求
为坐标原点,试求![]() 的面积
的面积![]() 与
与![]() 之间的函数关系式,并求出自变量的取值范围.
之间的函数关系式,并求出自变量的取值范围.
![]() 是否存在这样的点
是否存在这样的点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.
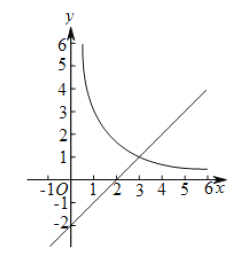
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家、食堂,图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家,如图反映了这个过程中,小明离家的距离y(km)与时间x(min)之间的对应关系,根据图象,下列说法正确的是( )
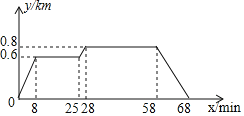
A.小明吃早餐用了25min
B.食堂到图书馆的距离为0.6km
C.小明读报用了30min
D.小明从图书馆回家的速度为0.8km/min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,AB=AC=2,∠BAC=90°,点D是AC的中点,点P是BC边上的动点,连接PA、PD.则PA+PD的最小值为( )
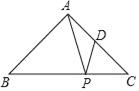
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(2,3),B(﹣3,n)两点,与x轴交于点C.
的图象交于点A(2,3),B(﹣3,n)两点,与x轴交于点C.
(1)求直线和双曲线的函数关系式.
(2)若kx+b﹣![]() <0,请根据图象直接写出x的取值范围.
<0,请根据图象直接写出x的取值范围.
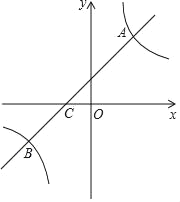
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小帆同学根据函数的学习经验,对函数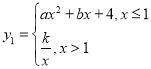 进行探究,已知函数过
进行探究,已知函数过![]() ,
,![]() ,
,![]() .
.
(1)求函数![]() 解析式;
解析式;
(2)如图1,在平面直角坐标系中画![]() 的图象,根据函数图象,写出函数的一条性质 ;
的图象,根据函数图象,写出函数的一条性质 ;
(3)结合函数图象回答下列问题:
①方程![]() 的近似解的取值范围(精确到个位)是 ;
的近似解的取值范围(精确到个位)是 ;
②若一次函数![]() 与
与![]() 有且仅有两个交点,则
有且仅有两个交点,则![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与轴,
与轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .抛物线
.抛物线![]() 经过点
经过点![]() ,将点
,将点![]() 向右平移
向右平移![]() 个单位长度,得到点
个单位长度,得到点![]() .
.
(1)求点![]() 的坐标和抛物线的对称轴;
的坐标和抛物线的对称轴;
(2)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com