
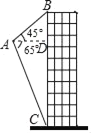
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为65°,此时航拍无人机A处与该建筑物的水平距离AD为80米.求该建筑物的高度BC(精确到1米).(参考数据:sin65°=0.91,cos65°=0.42,tan65°=2.14)
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
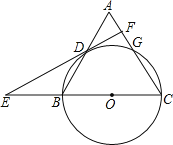
【题目】如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.
(1)求证:DF⊥AC;
(2)求tan∠E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】外线投资是篮球队常规训练的重要项目之一,下列图表中数据是甲乙丙三从每从十次投篮测试的成绩,测试规则为连续投篮十个球为一次,投进篮筐一个球记为1分.
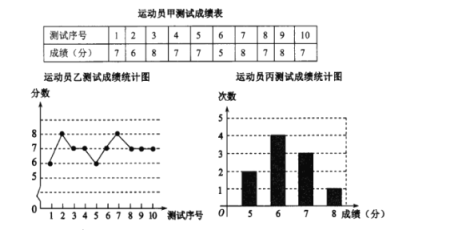
(1)写出运动员乙测试成绩的众数和中位数;
(2)在他们三从中选择一位投篮成绩优秀且较为稳定的选手作为中锋,你认为选谁更合适?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=3cm,BC=4cm,点E是BC上一点,且CE=1cm.点P由点C出发,沿CD方向向点D匀速运动,速度为1cm/s;点Q由点A出发,沿AD方向向点D匀速运动,速度为![]() cm/s,点P,Q同时出发,PQ交BD于F,连接PE,QB,设运动时间为t(s)(0<t<3).
cm/s,点P,Q同时出发,PQ交BD于F,连接PE,QB,设运动时间为t(s)(0<t<3).
(1)当t为何值时,PE∥BD?
(2)设△FQD的面积为y(cm2),求y与t之间的函数关系式.
(3)是否存在某一时刻t,使得四边形BQPE的周长最小.若存在,求出此四边形BQPE的面积;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有![]() 名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
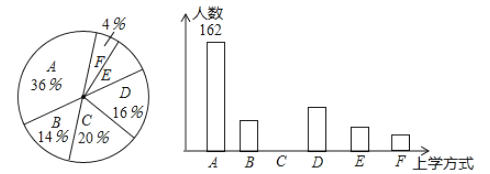
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有_____人,其中选择![]() 类的人数有_____人;
类的人数有_____人;
(2)在扇形统计图中,求![]() 类对应的扇形圆心角
类对应的扇形圆心角![]() 的度数,并补全条形统计图;
的度数,并补全条形统计图;
(3)若将![]() 这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知在平面直角坐标系![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别为坐标轴上的三个点,且
分别为坐标轴上的三个点,且![]() ,
,![]() ,
,![]() .
.
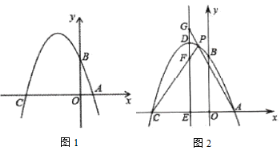
(1)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)点![]() 是抛物线上一个动点,且在直线
是抛物线上一个动点,且在直线![]() 的上方,连接
的上方,连接![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点,使四边形
,那么是否存在点,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图2,过抛物线顶点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() 、
、![]() 两点间的一个动点(点
两点间的一个动点(点![]() 不与
不与![]() 、
、![]() 两点重合),直线
两点重合),直线![]() 、
、![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 、
、![]() ,当点
,当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点
的图象过点![]() 且与直线
且与直线![]() 相交于
相交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上.
轴上.
![]() 求二次函数的解析式.
求二次函数的解析式.
![]() 如果
如果![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 为坐标原点,试求
为坐标原点,试求![]() 的面积
的面积![]() 与
与![]() 之间的函数关系式,并求出自变量的取值范围.
之间的函数关系式,并求出自变量的取值范围.
![]() 是否存在这样的点
是否存在这样的点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.
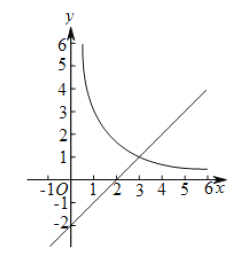
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小帆同学根据函数的学习经验,对函数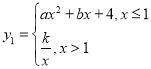 进行探究,已知函数过
进行探究,已知函数过![]() ,
,![]() ,
,![]() .
.
(1)求函数![]() 解析式;
解析式;
(2)如图1,在平面直角坐标系中画![]() 的图象,根据函数图象,写出函数的一条性质 ;
的图象,根据函数图象,写出函数的一条性质 ;
(3)结合函数图象回答下列问题:
①方程![]() 的近似解的取值范围(精确到个位)是 ;
的近似解的取值范围(精确到个位)是 ;
②若一次函数![]() 与
与![]() 有且仅有两个交点,则
有且仅有两个交点,则![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com