
【题目】如图,已知抛物线y=![]() x2-
x2-![]() x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.

(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)A点坐标为(4,0),D点坐标为(-2,0),C点坐标为(0,-3);
(2)M点坐标为(2,-3)或(1+![]() ,3)或(1-
,3)或(1-![]() ,3);
,3);
(3)在抛物线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(-2,0)或(6,6).
【解析】试题分析:(1)在![]() 中令
中令![]() ,解得
,解得![]() ,
,
∴A(4,0) 、D(-2,0).
在![]() 中令
中令![]() ,得
,得![]() ,∴C(0,-3).
,∴C(0,-3).
(2)连接AC,根据轴对称的性质,AC与抛物线的对称轴交点M即为所求,从而应用待定系数法求出AC的解析式,再求出抛物线的对称轴,即可求得点M的坐标.
(3)分BC为梯形的底边和BC为梯形的腰两种情况讨论即可.
试题解析:(1)A(4,0) 、D(-2,0)、C(0,-3)
(2)如图,连接AC,则AC与抛物线的对称轴交点M即为所求.
设直线AC的解析式为![]() ,则
,则![]() ,解得
,解得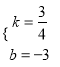 .
.
∴直线AC的解析式为![]() .
.
∵![]() 的对称轴是直线
的对称轴是直线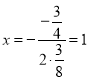 ,
,
把x=1代入![]() 得
得![]()
`∴M(1, ![]() ).
).
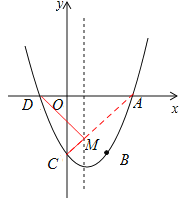
(3)存在,分两种情况:
①如图,当BC为梯形的底边时,点P与D重合时,四边形ADCB是梯形,此时点P为(-2,0).
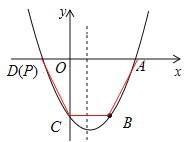
②如图,当BC为梯形的腰时,过点C作CP//AB,与抛物线交于点P,
∵点C,B关于抛物线对称,∴B(2,-3)
设直线AB的解析式为![]() ,则
,则![]() ,解得
,解得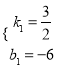 .
.
∴直线AB的解析式为![]() .
.
∵CP//AB,∴可设直线CP的解析式为![]() .
.
∵点C在直线CP上,∴![]() .
.
∴直线CP的解析式为![]() .
.
联立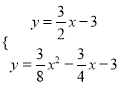 ,解得
,解得![]() ,
, ![]()
∴P(6,6).
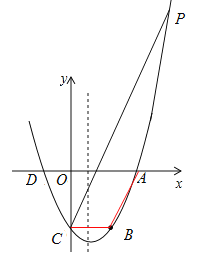
综上所述,在抛物线上存在点P,使得以A、B、C、P四点为顶点的四边形为梯形,点P的坐标为(-2,0)或(6,6).


科目:初中数学 来源: 题型:
【题目】某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
日销售单价x(元) | 3 | 4 | 5 | 6 |
日销售量y(个) | 20 | 15 | 12 | 10 |
(1)猜测并确定y与x之间的函数关系式,并画出图象;
(2)设经营此贺卡的销售利润为W元,求出W与x之间的函数关系式,
(3)若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价x定为多少时,才能获得最大日销售利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③AM平分∠ADF;④AB+AC=2AE;其中正确的有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)画出二次函数y=x2+bx+c的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm.点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,设运动时间为x秒,△PBQ的面积为y(cm2).

(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从4月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表:
一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
不超过150度 |
|
超过150度的部分 |
|
今年5月份,该市居民甲用电100度,交电费60元;居民乙用电200度,交电费122.5元.
(1)上表中,![]() ,
,![]() ;
;
(2)试行“阶梯电价”收费以后,该市一户居民今年8月份平均电价每度为0.63元,求该用户8月用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组).一元一次不等式和一次函数后,对相关知识进行了归纳整理.
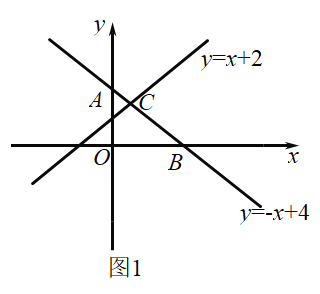
(1)例如,他在同一个直角坐标系中画出了一次函数y=x+2和y=-x+4的图像(如图1),并作了归纳:
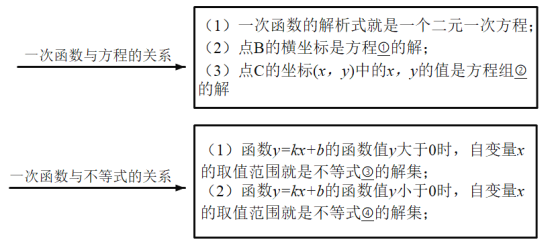
请根据图1和以上方框中的内容,在下面数字序号后写出相应的结论:
① ;② ;
③ ;④ ;
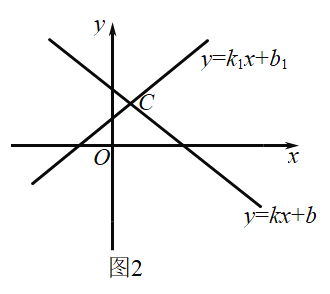
(2)若已知一次函数y=k1x+b1和y=kx+b的图像(如图2),且它们的交点C的坐标为(1,3),那么不等式kx+b≥k1x+b1的解集 .
查看答案和解析>>
科目:初中数学 来源: 题型:
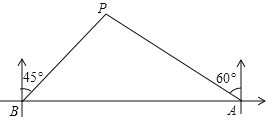
【题目】如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com