
【题目】本题满分11分.
如图,已知直线y=-![]() x +3分别与x、y轴交于点A和B.
x +3分别与x、y轴交于点A和B.
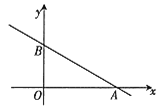
(1)求点A、B的坐标;
(2)求原点O到直线l的距离;
(3)若圆M的半径为2,圆心M在y轴上,当圆M与直线l相切时,求点M的坐标.
【答案】(1)A(4,0)、B(0,3)(2)![]() (3)M(0,
(3)M(0,![]() )或 M(0,
)或 M(0,![]() )
)
【解析】
(1)根据x轴、y轴上的点的特点可以直接求解;
(2)根据点到直线的距离是点到直线的垂线段的长,因此过点O作OC⊥AB于点C,然后根据三角形的面积法可求得距离;
(3)过M作MD⊥AB交AB于点D,然后可通过三角形相似可直接结果,但是由于M点在y轴上移动,因此可知在直线的上方和下方都会相切,因此分两种情况讨论求解.
解:(1)当x=0时,y=3
∴B点坐标(0,3)
当y=0时,有0=-![]() x + 3,
x + 3,
解得x=4
∴A点坐标为(4,0)
(2)过点O作OC⊥AB于点C,
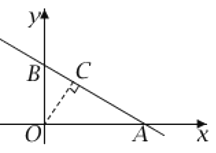
则OC长为原点O到直线l的距离
在Rt△BOA中,0A=4,0B=3,由勾股定理可得AB=5,
∵S△BOA=![]() OB×OA=
OB×OA=![]() AB×OC
AB×OC
∴OC=![]() =
=![]()
∴原点O到直线l的距离为![]()
(3)
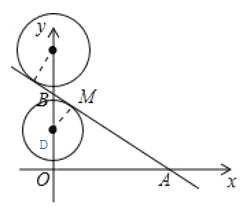
过M作MD⊥AB交AB于点D,当圆M与直线l相切时,MD=2,
在△BOA和△BDM中,
∵∠OBA=∠DBM,∠BOA=∠BDM
∴△BOA∽△BDM
∴![]() =
=![]() ,
,
∴BM=![]() =
=![]()
∴ OM=OB–BM=![]()
或OM=OB+ BM=![]()
∴点M的坐标为M(0,![]() )或 M(0,
)或 M(0,![]() )
)


科目:初中数学 来源: 题型:
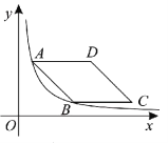
【题目】如图,在平面直角坐标系中,菱形![]() 在第一象限内,边
在第一象限内,边![]() 与
与![]() 轴平行,
轴平行,![]() ,
,![]() 两点的纵坐标分别为
两点的纵坐标分别为![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,菱形
两点,菱形![]() 的面积为
的面积为![]() ,则
,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
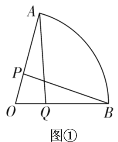
【题目】在扇形![]() 中,
中,![]() ,半径
,半径![]() ,点P为
,点P为![]() 上任一点(不与A、O重合).
上任一点(不与A、O重合).
(1)如图①,Q是![]() 上一点,若
上一点,若![]() ,求证:
,求证:![]() .
.
(2)如图②,将扇形沿![]() 折叠,得到O的对称点
折叠,得到O的对称点![]() .
.
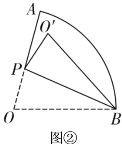
①若点![]() 落在
落在![]() 上,求
上,求![]() 的长;
的长;
②当![]() 与扇形
与扇形![]() 所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王芳同学到文具店购买中性笔和笔记本,中性笔每支1元,笔记本每本3元,王芳同学现有10元钱,则可供她选择的购买方案的个数为(两样都买,余下的钱少于1元)( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
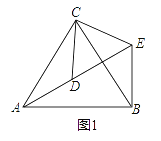
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
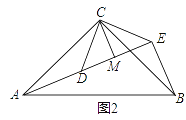
(3)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把分子为1的分数叫做单位分数,如:![]() ,
,![]() ,
,![]() ,任何一个单位分数都可以拆分成两个不同的单位分数的和,如“
,任何一个单位分数都可以拆分成两个不同的单位分数的和,如“![]() =
=![]() +
+![]() ”,“
”,“![]() =
=![]() +
+![]() ”……
”……
(1)根据对上述式子的观察,你会发现.![]() =
=![]() ·请将问题中的空格补充完整.
·请将问题中的空格补充完整.
(2)进一步思考,单位分数![]() (n是不小于2的正整数),请写出■和●所表示的代数式,并对你的结论进行验证.
(n是不小于2的正整数),请写出■和●所表示的代数式,并对你的结论进行验证.
(3)请用(2)中你找出的规律解方程![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
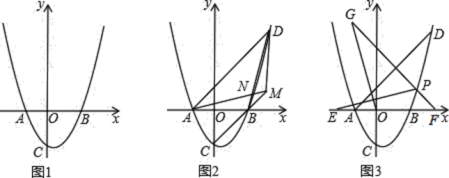
【题目】在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 分别交
分别交![]() 轴正半轴于点
轴正半轴于点![]() ,交
,交![]() 轴负半轴于点
轴负半轴于点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,且
,且![]() .
.
(1)如图1,求![]() 的值;
的值;
(2)如图![]() ,
,![]() 是第一象限抛物线上的点,连
是第一象限抛物线上的点,连![]() ,过点
,过点![]() 作
作![]() 轴,交
轴,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标以及
的坐标以及![]() 的值;
的值;
(3)如图3,在(2)的条件下,连接![]() ,
,![]() 是第一象限抛物线上的点(点
是第一象限抛物线上的点(点![]() 与点
与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,点
,点![]() 在直线
在直线![]() 上,连接
上,连接![]() 、
、![]() .若
.若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年3月,我国湖北省A、B两市遭受严重新冠肺炎影响,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)经过当地政府的大力支持,从D市到B市的运输时间缩短了,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com