
.如图,在菱形ABCD中,过点A作AE⊥BC,垂足E为BC中点,连接DE,F为DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=2,求AF的长.

【考点】相似三角形的判定与性质;菱形的性质.
【分析】(1)由菱形的性质得出AD∥BC,AB∥CD,得出∠ADF=∠DEC,∠B+∠C=180°,再由已知条件和邻补角关系求出∠AFD=∠C,即可得出结论;
(2)由菱形的性质得出AD=AB=BC=2,由勾股定理求出AE、DE,再由相似三角形的性质得出对应边成比例,即可求出AF的长.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠DEC,∠B+∠C=180°,
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)解:∵四边形ABCD是菱形,
∴AD=AB=BC=2,
∵AE⊥BC,E为BC中点,
∴AE⊥AD,BE= BC=1,
BC=1,
∴∠DAE=90°,AE=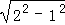 =
= ,
,
∴DE=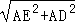 =
= ,
,
∵△ADF∽△DEC,
∴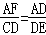 ,
,
即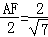 ,
,
解得:AF=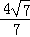 .
.
【点评】本题考查了菱形的性质、相似三角形的判定与性质、勾股定理;熟练掌握菱形的性质,并能进行推理论证与计算是解决问题的关键.


科目:初中数学 来源: 题型:
老师在黑板上出了一道题,是一个多项式减去2x2﹣3x+5,小明由于粗心大意,将减号抄成了加号,计算出的结果是4x2+3x﹣1,请你求出老师出的这道题的正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
在四边形ABCD中,(1)AB∥CD,(2)AD∥BC,(3)AB=CD,(4)AD=BC,在这四个条件中任选两个作为已知条件,能判定四边形ABCD是平行 四边形的概率是______
四边形的概率是______
__
查看答案和解析>>
科目:初中数学 来源: 题型:
在Rt△ABC中,∠BAC=90°,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得△AFB,连接EF,下列结论:
①△AED≌△AEF;②△ABC的面积等于四边形AFBD的面积:③BE+DC=DE;
④BE2+DC2=DE2; ⑤∠DAC=22.5°,其中正确的是 ( )
A.①③④ B.③④⑤ C.①②④ D.①②⑤

查看答案和解析>>
科目:初中数学 来源: 题型:
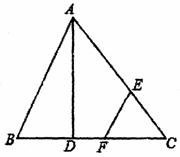
如图,已知点D、F分别是△ABC的 边BC上两点,点E是边AC上一点,∠BFE=∠FEA,AB=13,AD=12,BD=5,AE=10,DF=4.
(1) 求证:AD⊥BC;
(2) 求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com