
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=4![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.

【答案】(1)四边形EBGD是菱形.理由见解析;(2)4![]()
【解析】试题分析:(1)结论四边形EBGD是菱形.只要证明BE=ED=DG=GB即可.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在Rt△EMC中,求出EM、MC即可解决问题.
试题解析:
(1)四边形EBGD是菱形.理由:
∵EG垂直平分BD,
∴EB=ED,GB=GD,BF=DF.
∴∠EBD=∠EDB.
又∵∠EBD=∠DBC,
∴∠EDF=∠GBF.
在△EFD和△GFB中,
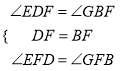
∴△EFD≌△GFB(ASA).
∴ED=BG.
∴BE=ED=DG=GB.
∴四边形EBGD是菱形.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小.
在Rt△EBM中,
∵∠EMB=90°,∠EBM=30°,EB=ED=4![]() ,
,
∴EM=![]() BE=2
BE=2![]() .
.
∵DE∥BC,EM⊥BC,DN⊥BC,
∴EM∥DN,EM=DN=2![]() ,MN=DE=4
,MN=DE=4![]() .
.
在Rt△DNC中,∵∠DNC=90°,∠DCN=45°,
∴∠NDC=∠NCD=45°.
∴DN=NC=2![]() .
.
∴MC=4![]() +2
+2![]() =6
=6![]() .
.
在Rt△EMC中,∵∠EMC=90°,由勾股定理,得EC=![]() .
.
∵HG+HC=EH+HC=EC,
∴HG+HC的最小值为4![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC的周长是10,求□ABCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道“在同一平面内,经过直线外一点有且只有一条直线与已知直线平行”,

小伟同学想通过“同位角相等,两直线平行”作出图形,具体作法是,过点P任意作一条直线a与直线l相交,再以P为顶点作一个角,直线a为角的一边所在直线,则角的另一边所在直线与直线l平行.
(1)请你参照小伟同学的作法,帮他完成剩余的作图(保留作图痕迹,不写作法)
(2)你还有其它办法吗?请在备用图中完成(只需一种即可,保留作图痕迹,不写作法)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A. 线段是轴对称图形
B. 等边三角形有3条对称轴
C. 角只有一条对称轴,是这个角的角平分线
D. 底与腰不相等的等腰三角形只有一条对称轴
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com