
【题目】我们把顺次连接四边形各边中点所得的四边形叫做中点四边形.若一个任意四边形的面积为a,则它的中点四边形面积为( )
A.![]() aB.
aB. ![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
由E为AB中点,且EF平行于AC,EH平行于BD,得到△BEK与△ABM相似,△AEN与△ABM相似,利用面积之比等于相似比的平方,得到△EBK面积与△ABM面积之比为1:4,且△AEN与△EBK面积相等,进而确定出四边形EKMN面积为△ABM的一半,同理得到四边形KFPM面积为△BCM面积的一半,四边形QGPM面积为△DCM面积的一半,四边形HQMN面积为△DAM面积的一半,四个四边形面积之和即为四个三角形面积之和的一半,即为四边形ABCD面积的一半,即可得出答案.
解:如图,画任意四边形ABCD,设AC与EH,FG分别交于点N,P,BD与EF,HG分别交于点K,Q,则四边形EFGH即为它的中点四边形,

∵E是AB的中点,EF//AC,EH//BD,
∴△EBK∽△ABM,△AEN∽△ABM,
∴![]() =
=![]() ,S△AEN=S△EBK,
,S△AEN=S△EBK,
∴![]() =
=![]() ,
,
同理可得:![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵四边形ABCD的面积为a,
∴四边形EFGH的面积为![]() ,
,
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】![]() 三点在数轴上,点
三点在数轴上,点![]() 表示的数是
表示的数是![]() ,从点
,从点![]() 出发向右平移7个单位长度得到点
出发向右平移7个单位长度得到点![]() 。
。
(1)求出点![]() 表示的数,画一条数轴并在数轴上标出点
表示的数,画一条数轴并在数轴上标出点![]() 和点
和点![]() ;
;
(2)若此数轴在一张纸上,将纸沿某一条直线对折,此时![]() 点与表示数
点与表示数![]() 的点刚好重合,折痕与数轴有一个交点
的点刚好重合,折痕与数轴有一个交点![]() ,求点
,求点![]() 表示的数的相反数(原卷无此问);
表示的数的相反数(原卷无此问);
(3)在数轴上有一点![]() ,点
,点![]() 到点
到点![]() 和点
和点![]() 的距离之和为11,求点
的距离之和为11,求点![]() 所表示的数;
所表示的数;
(4)![]() 从初始位置分别以1单位长度
从初始位置分别以1单位长度![]() 和2单位长度
和2单位长度![]() 的速度同时向左运动,是否存在
的速度同时向左运动,是否存在![]() 的值,使
的值,使![]() 秒后点
秒后点![]() 到
到![]() 的距离与点
的距离与点![]() 到原点距离相等?若存在请求出
到原点距离相等?若存在请求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 与菱形
与菱形![]() 在平面直角坐标系中,点
在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 在点
在点![]() 的右侧.
的右侧.


(![]() )求菱形
)求菱形![]() 的周长.
的周长.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 轴向右以每秒
轴向右以每秒![]() 个单位长度的速度平移,菱形
个单位长度的速度平移,菱形![]() 沿
沿![]() 轴向左以每秒
轴向左以每秒![]() 个单位长度的速度平移,设菱形移动的时间为(
个单位长度的速度平移,设菱形移动的时间为(![]() 秒),当⊙
秒),当⊙![]() 与
与![]() 相切,且切点为
相切,且切点为![]() 的中点时,连接
的中点时,连接![]() ,求
,求![]() 的值及
的值及![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,当点
)的条件下,当点![]() 与
与![]() 所在的直线的距离为
所在的直线的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣![]() +bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为(﹣2,0).
+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为(﹣2,0).
(1)求抛物线的解析式;
(2)连接AC、BC,求线段BC所在直线的解析式;
(3)在抛物线的对称轴上是否存在点P,使△ACP为等腰三角形?若存在,求出符合条件的P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”.
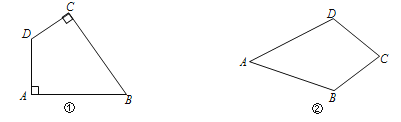
(1)如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上);

(2)下列说法正确的有 ;(填写所有正确结论的序号)
①一组对边平行的“准矩形”是矩形;②一组对边相等的“准矩形”是矩形;
③一组对边相等的“准菱形”是菱形;④一组对边平行的“准菱形”是菱形.
(3)如图⑤,在△ABC中,∠ABC=90°,以AC为一边向外作“准菱形”ACEF,且AC=EC,AF=EF,AE、CF交于点D.
①若∠ACE=∠AFE,求证:“准菱形”ACEF是菱形;
②在①的条件下,连接BD,若BD=![]() ,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.
,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高中学生身体素质,学校开设了A:篮球、B:足球、C:跳绳、D:羽毛球四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校随机抽取若干名学生进行问卷调查(每个被调查的对象必须选择而且只能在四种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图(未画完整).

(1)这次调查中,一共调查了________名学生;
(2)请补全两幅统计图;
(3)若有3名喜欢跳绳的学生,1名喜欢足球的学生组队外出参加一次联谊活动,欲从中选出2人担任组长(不分正副),求一人是喜欢跳绳、一人是喜欢足球的学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com