
如图,二次函数y=ax2+bx+3的图象与x轴相交于点A(﹣3,0)、B(1,0),与y轴相交于点C,点G是二次函数图象的顶点,直线GC交x轴于点H(3,0),AD平行GC交y轴于点D.
(1)求该二次函数的表达式;
(2)求证:四边形ACHD是正方形;
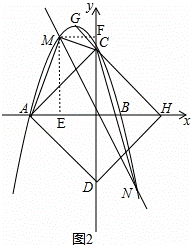
(3)如图2,点M(t,p)是该二次函数图象上的动点,并且点M在第二象限内,过点M的直线y=kx交二次函数的图象于另一点N.
①若四边形ADCM的面积为S,请求出S关于t的函数表达式,并写出t的取值范围;
②若△CMN的面积等于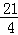 ,请求出此时①中S的值.
,请求出此时①中S的值.

解:(1)∵二次函数y=ax2+bx+3的图象与x轴相交于点A(﹣3,0)、B(1,0),
∴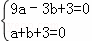
解得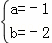
∴二次函数的表达式为y=﹣x2﹣2x+3.
(2)如图1,
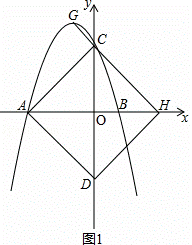 ,
,
∵二次函数的表达式为y=﹣x2﹣2x+3,
∴点C的坐标为(0,3),
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴点G的坐标是(﹣1,4),
∵点C的坐标为(0,3),
∴设CG所在的直线的解析式是y=mx+3,
则﹣m+3=4,
∴m=﹣1,
∴CG所在的直线的解析式是y=﹣x+3,
∴点H的坐标是(3,0),
设点D的坐标是(0,p),
则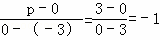 ,
,
∴p=﹣3,
∵AO=CO=DO=HO=3,AH⊥CD,
∴四边形ACHD是正方形.
(3)①如图2,作ME⊥x轴于点E,作MF⊥y轴于点F,
 ,
,
∵四边形ADCM的面积为S,
∴S=S四边形AOCM+S△AOD,
∵AO=OD=3,
∴S△AOD=3×3÷2=4.5,
∵点M(t,p)是y=kx与y=﹣x2﹣2x+3在第二象限内的交点,
∴点M的坐标是(t,﹣t2﹣2t+3),
∵ME=﹣t2﹣2t+3,MF=﹣t,
∴S四边形AOCM=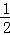 ×3×(﹣t2﹣2t+3)
×3×(﹣t2﹣2t+3)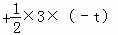 =﹣
=﹣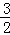 t2﹣
t2﹣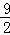 t+
t+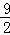 ,
,
∴S=﹣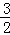 t2﹣
t2﹣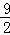 t+
t+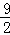 +4.5=﹣
+4.5=﹣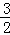 t2﹣
t2﹣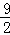 t+9,﹣3<t<0.
t+9,﹣3<t<0.
②如图3,作NI⊥x轴于点I,
 ,
,
设点N的坐标是(t1,p1),
则NI=|t1|,
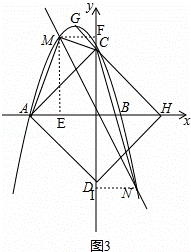
∴S△CMN=S△COM+S△CON=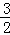 (|t|+|t1|),
(|t|+|t1|),
∵t<0,t1>0,
∴S△CMN=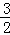 (|t|+|t1|)=
(|t|+|t1|)=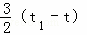 =
=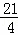 ,
,
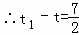 ,
,
联立
可得x2﹣(k+2)x﹣3=0,
∵t1、t是方程的两个根,
∴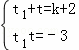
∴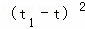 =
=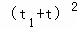 ﹣4t1t=(k+2)2﹣4×(﹣3)=
﹣4t1t=(k+2)2﹣4×(﹣3)=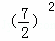 =
=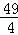 ,
,
解得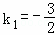 ,
,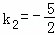 ,
,
a、k=﹣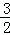 时,
时,
由x2+(2﹣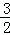 )x﹣3=0,
)x﹣3=0,
解得x1=﹣2,或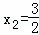 (舍去).
(舍去).
b、k=﹣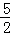 时,
时,
由x2+(2﹣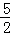 )x﹣3=0,
)x﹣3=0,
解得x3=﹣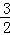 ,或x4=2(舍去),
,或x4=2(舍去),
∴t=﹣2,或t=﹣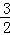 ,
,
t=﹣2时,
S=﹣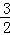 t2﹣
t2﹣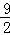 t+9
t+9
=﹣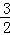 ×4﹣
×4﹣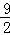 ×(﹣2)+9
×(﹣2)+9
=12
t=﹣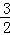 时,
时,
S=﹣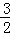 ×
×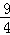 ﹣
﹣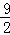 ×
×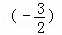 +9
+9
=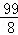 ,
,
∴S的值是12或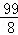 .
.


科目:初中数学 来源: 题型:
湘西自治州风景优美,物产丰富,一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产.若购买3盒豆腐乳和2盒猕猴桃果汁共需180元;购买1盒豆腐乳和3盒猕猴桃果汁共需165元.
(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;
(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
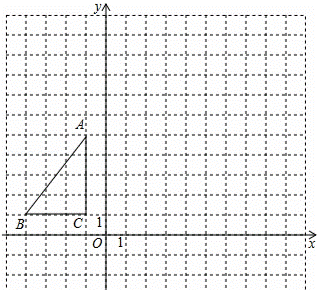
如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,
(1)画出△AB′C′;
(2)写出点B′,C′的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
据统计,2009年漳州市报名参加中考总人数(含八年级)约为102 000人,则102 000用科学记数法表示
为( )
A. 0.102×106 B. 1.02×105 C. 10.2×104 D. 102×103
查看答案和解析>>
科目:初中数学 来源: 题型:
二次函数y=﹣x2+(3+k)x+2k﹣1的图象与y轴的交点位于(0,5)上方,则k的范围是( )
A. k=3 B. k<3 C. k>3 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
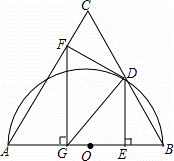
如图,已知等边△ABC,以AB为直径的半圆与BC边交于点D,过点D作⊙O的切线DF交AC于点F,过点D作DE⊥AB,垂足为点E,过点F作FG⊥AB,垂足为点G,连结GD.
(1)求证:DF⊥AC;
(2)若AB=8,求tan∠FGD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com