
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.
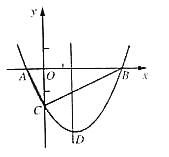
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
(3)点![]() 是抛物线对称轴上的一个动点,当
是抛物线对称轴上的一个动点,当![]() 周长最小时,求点
周长最小时,求点![]() 的坐标及
的坐标及![]() 的最小周长.
的最小周长.
【答案】(1)![]() ,D
,D![]() ;(2)
;(2)![]() 是直角三角形,见解析;(3)
是直角三角形,见解析;(3)![]() ,
,![]() .
.
【解析】
(1)直接将(1,0),代入解析式进而得出答案,再利用配方法求出函数顶点坐标;
(2)分别求出AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,进而利用勾股定理的逆定理得出即可;
(3)利用轴对称最短路线求法得出M点位置,求出直线![]() 的解析式,可得M点坐标,然后易求此时△ACM的周长.
的解析式,可得M点坐标,然后易求此时△ACM的周长.
解:(1)∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,
,
解得:![]() .
.
∴抛物线的解析式为![]() ,
,
∵![]() ,
,
∴顶点![]() 的坐标为:
的坐标为:![]() ;
;
(2)![]() 是直角三角形,
是直角三角形,
证明:当![]() 时
时![]() ,
,
∴![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形;
是直角三角形;
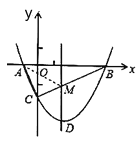
(3)如图所示:BC与对称轴交于点M,连接![]() ,
,
根据轴对称性及两点之间线段最短可知,此时![]() 的值最小,即
的值最小,即![]() 周长最小,
周长最小,
设直线![]() 解析式为:
解析式为:![]() ,则
,则![]() ,
,
解得: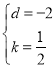 ,
,
故直线![]() 的解析式为:
的解析式为:![]() ,
,
∵抛物线对称轴为![]()
∴当![]() 时,
时,![]() ,
,
∴![]() ,
,
![]() 最小周长是:
最小周长是:![]() .
.


科目:初中数学 来源: 题型:
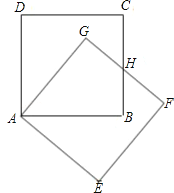
【题目】把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
,![]() ,
,![]() ,点
,点![]() 是斜边的中点,以点
是斜边的中点,以点![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 、
、![]() 分别交边
分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
特例
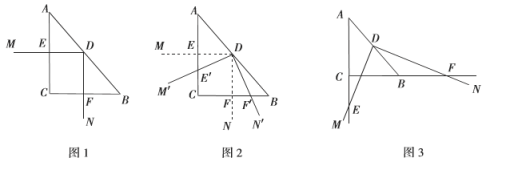
(1)如图1,若![]() ,不添加辅助线,图1中所有与
,不添加辅助线,图1中所有与![]() 相似的三角形为 ,
相似的三角形为 ,![]() ;
;
操作探究:
(2)将(1)中的![]() 从图1的位置开始绕点
从图1的位置开始绕点![]() 按逆时针方向旋转,得到
按逆时针方向旋转,得到![]() ,如图2,当射线
,如图2,当射线![]() ,
,![]() 分别交边
分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() 时,求
时,求![]() 的值;
的值;
拓展延伸:
(3)如图3,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点,以点
的中点,以点![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 、
、![]() 分别交边
分别交边![]() 、
、![]() 的延长线于点
的延长线于点![]() 、
、![]() ,则
,则![]() 的值为 .(用含
的值为 .(用含![]() 、
、![]() 的代数式表示,直接回答即可)
的代数式表示,直接回答即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
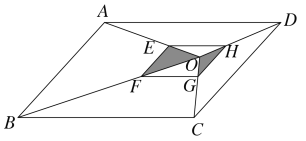
【题目】如图,四边形ABCD,EFGH都是平行四边形,点O是![]() 内的一点,点E、F、G,H分别是OA、OB、OC、OD上的一点,EF //AB,OA= 3OE,若阴影部分的面积为S,则
内的一点,点E、F、G,H分别是OA、OB、OC、OD上的一点,EF //AB,OA= 3OE,若阴影部分的面积为S,则![]() 的面积为( )
的面积为( )
A.6SB.18SC.24SD.32S
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,且OC2=OA·OB.
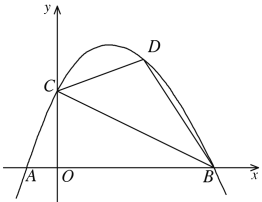
(1)证明:tan∠BAC· tan∠ABC=1;
(2)若点C的坐标为(0,2),tan∠OCB=2,
①求该抛物线的表达式;
②若点D是该抛物线上的一点,且位于直线BC上方,当四边形ABDC的面积最大时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
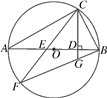
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是弧![]() 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
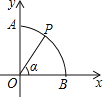
A. (sinα,sinα) B. (cosα,cosα) C. (cosα,sinα) D. (sinα,cosα)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: ①![]() =
=![]() ; ②
; ②![]() =
=![]() ;③
;③![]() =
=![]() ;④
;④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
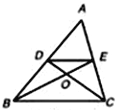
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com