
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,且OC2=OA·OB.
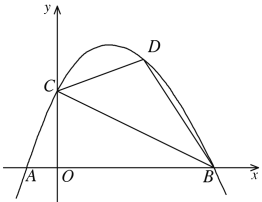
(1)证明:tan∠BAC· tan∠ABC=1;
(2)若点C的坐标为(0,2),tan∠OCB=2,
①求该抛物线的表达式;
②若点D是该抛物线上的一点,且位于直线BC上方,当四边形ABDC的面积最大时,求点D的坐标.
【答案】(1)见解析;(2)①![]() ,②D
,②D![]() .
.
【解析】
(1)由OC2=OA·OB和∠AOC=∠COB=90°,可判定△AOC∽△COB,可得∠BAC=∠OCB ,再根据正切的定义即可得证;
(2)①由C点坐标可得OC=2,然后由正切值求出OB,OA,即可得到A、B的坐标,然后采用待定系数法求函数表达式;
②连接AC,过D作DF⊥x轴,交直线BC于点E,设出D点坐标,先求出直线BC解析式,再根据D、E横坐标相同求出E点纵坐标,然后采用“铅锤法”可表示出△BCD的面积,因为△ABC固定,当△BCD面积最大时,则四边形ABDC面积最大.
解:(1)∵OC2=OA·OB
∴![]()
∵∠AOC=∠COB=90°
∴△AOC∽△COB
∴∠BAC=∠OCB
∴tan∠BAC=tan∠OCB=![]()
又∵tan∠ABC=![]()
∴tan∠BAC· tan∠ABC=1
(2)①∵点C的坐标为(0,2),tan∠OCB=2
∴OC=2,tan∠OCB=![]() =2
=2
∴OB=2OC=4,则B点坐标为(4,0)
又∵OC2=OA·OB
∴OA=![]() ,则A点坐标为(-1,0)
,则A点坐标为(-1,0)
将A(-1,0),B(4,0),C (0,2)代入二次函数表达式得,
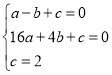 ,解得
,解得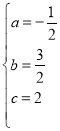 ,
,
∴二次函数表达式为![]()
②如图,连接AC,过D作DF⊥x轴,交直线BC于点E,
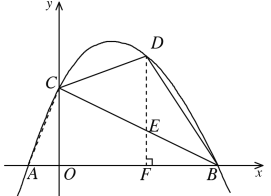
设BC直线解析式为![]() ,将B(4,0),C (0,2)代入得,
,将B(4,0),C (0,2)代入得,
![]() ,解得
,解得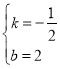 ,
,
∴BC直线解析式为![]()
设D点坐标为![]() ,
,
则E点横坐标为m,代入BC直线可得![]() ,
,
即E点坐标为![]()
∴DE=![]()
∴![]()
∵S四边形ABDC=S△ABC+S△BCD,且S△ABC为定值,
∴当S△BCD取得最大值时,S四边形ABDC取得最大值.
∵![]()
∴当m=2时,△BCD的面积最大值为4,此时S四边形ABDC取得最大值,
将x=2时,![]()
∴当四边形ABDC的面积最大时,D的坐标为![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
【题目】某自行车行销售甲、乙两种品牌的自行车,若购进甲品牌自行车5辆,乙品牌自行车6辆,需要进货款9500元,若购进甲品牌自行车3辆,乙品牌自行车2辆,需要进货款4500元.
(1)求甲、乙两种品牌自行车每辆进货价分别为多少元;
(2)今年夏天,车行决定购进甲、乙两种品牌自行车共50辆,在销售过程中,甲品牌自行车的利润率为![]() ,乙品牌自行车的利润率为
,乙品牌自行车的利润率为![]() ,若将所购进的自行车全部销售完毕后其利润不少于29500,那么此次最多购进多少辆乙种品牌自行车?
,若将所购进的自行车全部销售完毕后其利润不少于29500,那么此次最多购进多少辆乙种品牌自行车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅行社为吸引游客组团去黄满寨风景区旅游,推出了如下收费标准:如果人数不超过25人,人均旅游费用为:1000元;如果人数超过25人,每超过1人,人均旅游费用降低20元,但人均旅游费用不低于700元.某单位组织员工去黄满寨风景区旅游,共支付给旅行社旅游费用27000元,请问:
(1)该单位旅游人数超过25人吗?说明理由.
(2)这次共有多少名员工去黄满寨风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-4,0)、B(1,0),与y轴交于点C(0,-4),P是直线AC下方抛物线上的点,若△ACP的面积为6,则tan∠AOP的值为_____________
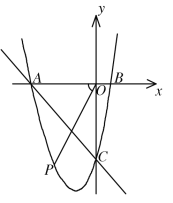
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.
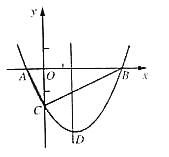
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
(3)点![]() 是抛物线对称轴上的一个动点,当
是抛物线对称轴上的一个动点,当![]() 周长最小时,求点
周长最小时,求点![]() 的坐标及
的坐标及![]() 的最小周长.
的最小周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.
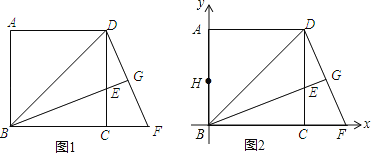
(1)求证:△BCE≌△DCF;
(2)求CF的长;
(3)如图2,在AB上取一点H,且BH=CF,若以BC为x轴,AB为y轴建立直角坐标系,问在直线BD上是否存在点P,使得以B、H、P为顶点的三角形为等腰三角形?若存在,直接写出所有符合条件的P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
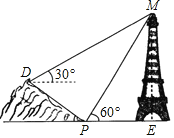
【题目】小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为![]() ,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为
,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为![]() .已知山坡坡度
.已知山坡坡度![]() ,即
,即![]() ,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据:
,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com