
【题目】已知,如图1,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.
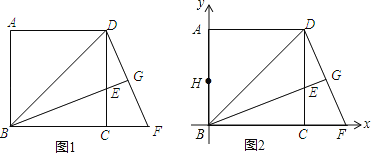
(1)求证:△BCE≌△DCF;
(2)求CF的长;
(3)如图2,在AB上取一点H,且BH=CF,若以BC为x轴,AB为y轴建立直角坐标系,问在直线BD上是否存在点P,使得以B、H、P为顶点的三角形为等腰三角形?若存在,直接写出所有符合条件的P点坐标;若不存在,说明理由.
【答案】(1)见解析;(2)![]() ﹣1;(3)所有符合条件的P点坐标为(2﹣
﹣1;(3)所有符合条件的P点坐标为(2﹣![]() ,2﹣
,2﹣![]() )、(﹣2+
)、(﹣2+![]() ,﹣2+
,﹣2+![]() )、(
)、(![]() ﹣1,
﹣1,![]() ﹣1)、(
﹣1)、(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用正方形的性质,由全等三角形的判定定理SAS即可证得△BCE≌△DCF;
(2)通过△DBG≌△FBG的对应边相等知BD=BF=![]() ;然后由CF=BF﹣BC=即可求得;
;然后由CF=BF﹣BC=即可求得;
(3)分三种情况分别讨论即可求得.
【解答】(1)证明:如图1,
在△BCE和△DCF中,
 ,
,
∴△BCE≌△DCF(SAS);
(2)证明:如图1,
∵BE平分∠DBC,OD是正方形ABCD的对角线,
∴∠EBC=![]() ∠DBC=22.5°,
∠DBC=22.5°,
由(1)知△BCE≌△DCF,
∴∠EBC=∠FDC=22.5°(全等三角形的对应角相等);
∴∠BGD=90°(三角形内角和定理),
∴∠BGF=90°;
在△DBG和△FBG中,
 ,
,
∴△DBG≌△FBG(ASA),
∴BD=BF,DG=FG(全等三角形的对应边相等),
∵BD=![]() =
=![]() ,
,
∴BF=![]() ,
,
∴CF=BF﹣BC=![]() ﹣1;
﹣1;
(3)解:如图2,∵CF=![]() ﹣1,BH=CF
﹣1,BH=CF
∴BH=![]() ﹣1,
﹣1,
①当BH=BP时,则BP=![]() ﹣1,
﹣1,
∵∠PBC=45°,
设P(x,x),
∴2x2=(![]() ﹣1)2,
﹣1)2,
解得x=2﹣![]() 或﹣2+
或﹣2+![]() ,
,
∴P(2﹣![]() ,2﹣
,2﹣![]() )或(﹣2+
)或(﹣2+![]() ,﹣2+
,﹣2+![]() );
);
②当BH=HP时,则HP=PB=![]() ﹣1,
﹣1,
∵∠ABD=45°,
∴△PBH是等腰直角三角形,
∴P(![]() ﹣1,
﹣1,![]() ﹣1);
﹣1);
③当PH=PB时,∵∠ABD=45°,
∴△PBH是等腰直角三角形,
∴P(![]() ,
,![]() ),
),
综上,在直线BD上是否存在点P,使得以B、H、P为顶点的三角形为等腰三角形,所有符合条件的P点坐标为(2﹣![]() ,2﹣
,2﹣![]() )、(﹣2+
)、(﹣2+![]() ,﹣2+
,﹣2+![]() )、(
)、(![]() ﹣1,
﹣1,![]() ﹣1)、(
﹣1)、(![]() ,
,![]() ).
).


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明![]() ;
;

【简单应用】
(2)阅读下面的内容,并解决后面的问题:如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数;

解:∵AP、CP分别平分∠BAD. ∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得: ![]()
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P =![]() (∠B+∠D)=26°.
(∠B+∠D)=26°.
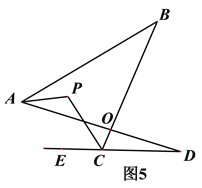
【问题探究】如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想![]() 的度数,并说明理由.
的度数,并说明理由.

【拓展延伸】
① 在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),
∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),

②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知水星的半径约为24 400 000米,用科学记数法表示为( )
A. 0.244 × l08米 B. 2.44×106米 C. 2.44×107米 D. 24.4×106米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com