
【题目】解下列方程:
(1)(2x-1)2=4
(2)![]() (用配方法)
(用配方法)
(3)x2+2x=4.
(4)![]()
【答案】
(1)解:∵(2x-1)2=4,
∴2x-1=2或2x-1=-2,
∴x1= ![]() ,x2=-
,x2=- ![]() ,
,
(2)解:∵x2-4x+1=0,
∴x2-4x+4=-1+4,
∴(x-2)2=3,
∴x1= ![]() , x2=
, x2= ![]() ,
,
(3)解:∵x2+2x=4,
∴x2+2x+1=4+1,
∴(x+1)2=5,
∴x1=-1+ ![]() ,x2=-1-
,x2=-1- ![]() ,
,
(4)解:∵2 ( x 3 ) 2 = x ( x 3 ),
∴(x-3)【2(x-3)-x】=0,
∴(x-3)(x-6)=0,
∴x1=3,x2=6,
【解析】(1)根据一元二次方程的解法——直接开平方法解方程即可.
(2)根据一元二次方程的解法——配方法和直接开平方法解方程即可.
(3)根据一元二次方程的解法——配方法和直接开平方法解方程即可.
(4)根据一元二次方程的解法——因式分解法解方程即可.
【考点精析】关于本题考查的直接开平方法和配方法,需要了解方程没有一次项,直接开方最理想.如果缺少常数项,因式分解没商量.b、c相等都为零,等根是零不要忘.b、c同时不为零,因式分解或配方,也可直接套公式,因题而异择良方;左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】已知:△ABC,点M是平面上一点,射线BM与直线AC交于点D,射线CM与直线AB交于点E.过点A作AF∥CE,AF与BC所在的直线交于点F.

(1)如图1,当BD⊥AC,CE⊥AB时,写出∠BAD的一个余角,并证明∠ABD=∠CAF;
(2)若∠BAC=80°,∠BMC=120°.
①如图2,当点M在△ABC内部时,用等式表示∠ABD与∠CAF之间的数量关系,并加以证明;
②如图3,当点M在△ABC外部时,依题意补全图形,并直接写出用等式表示的∠ABD与∠CAF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
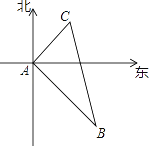
【题目】如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,请你求出乙船的航行方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
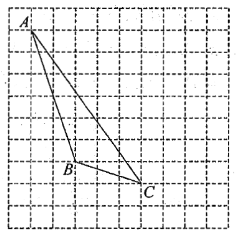
【题目】如图,在方格纸内将![]() 水平向右平移4个单位得到
水平向右平移4个单位得到![]() .
.
(1)补全![]() ,利用网格点和直尺画图;
,利用网格点和直尺画图;
(2)图中![]() 与
与![]() 的位置关系是: ;
的位置关系是: ;
(3)画出![]() 中
中![]() 边上的中线
边上的中线![]() ;
;
(4)平移过程中,线段![]() 扫过的面积是: .
扫过的面积是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】细心观察图形,认真分析各式,然后解答问题.
OA22=![]() ,
,![]() ;
;
OA32=12+![]() ,
,![]() ;
;
OA42=12+![]() ,
,![]() …
…
(1)请用含有n(n是正整数)的等式表示上述变规律:OAn2等于多少;Sn等于多少.
(2)求出OA10的长.
(3)若一个三角形的面积是![]() ,计算说明他是第几个三角形?
,计算说明他是第几个三角形?
(4)求出S12+S22+S32+…+S102的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com